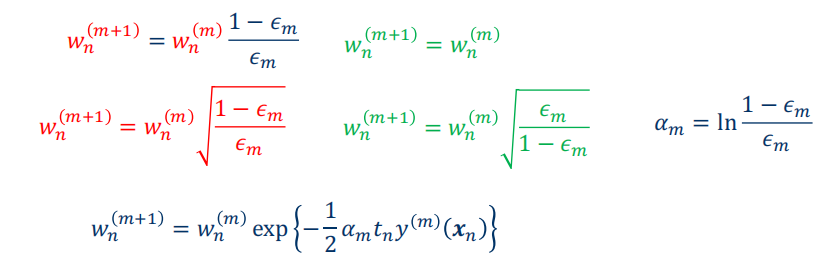跳转至

9 Ensemble Methods

The Bagging Algorithm (Bootstrap Aggregating)

  1. bootstrap: re-sample N examples from D uniformly with replacement
  2. aggregating: aggregate the outputs of the base learners
  3. base learner应该对微小的改变敏感，有时甚至允许过拟合
  4. base learner我们希望选择low bias的
  5. Parallel ensemble method

Random Forest

  1. use decision tree as basic unit in bagging, an ensemble model

  2. 决策树优点：处理缺失值、对输入空间的异常值鲁棒、速度快、可解释性高，非线性

  3. 决策树缺点：准确率低，容易过拟合

  4. process：随机采样N samples，重复T次，用这T个训练集独立训练出T个model

  5. aggregating all models will fuzzy up the decision boundary, helping reduce the variance

  6. RF incorporate randomized feature selection at each split step

    每次随机选择一部分特征用以训练决策树，即两重随机

    Each time, basic learner doesn’t learn from all data, but from Random bootstrap sampled data.

    只从一部分数据中学习

    Basic learner doesn’t use all features, but Random select some features.

    • more efficient
    • each time we only pick the best feature from size(f) rather than size(F).
    • we often let \(size(f)=\sqrt{k}\) in classification and \(\dfrac{k}{3}\) in regression

  7. 很显然地，每个树不比DT好，我们允许他们过拟合，以让他们aware little change，但组合起来可能更好

  8. 算法

    1. Select a new bootstrap sample from original training set
    2. Growing a tree…
    3. At each internal node, randomly select K features from ALL features and then, determine the best split in ONLY the K features. 每个结点仅选择K个特征计算信息增益得到最好的split
    4. Do not pruning
    5. Until Validation Error never decrease

Boosting

  • modify the weight of different training examples

如在跑第二个模型的时候，提高第一个模型分类错误的样本的权重

  • generate a model on the modified training set

  • sequential ensemble method

  • question 1: 如何改变样本权重让被分类错误的样本有更高权重

  • question 2：如何在final phase组合这些base learners

AdaBoost

  1. 初始权重设为\(1/N\)
  2. 对M个学习器，首先fit一个classifier最小化以下函数，其中I为符号函数，不等于就输出1，否则输出0
\[ J_{m}=\sum_{n=1}^{N}w_{n}^{(m)}I\left(y^{(m)}\left(x_{n}\right)\neq t_{n})\right) \]
  1. 评估错误率
\[ \epsilon_m=\frac{\sum_{n=1}^Nw_n^{(m)}I(y^{(m)}(x_n)\neq t_n)}{\sum_{n=1}^Nw_n^{(m)}} \]

​ 用 \(\alpha_m=\ln\dfrac{1-\epsilon_m}{\epsilon_m}\) 评估

  1. 更新权重系数

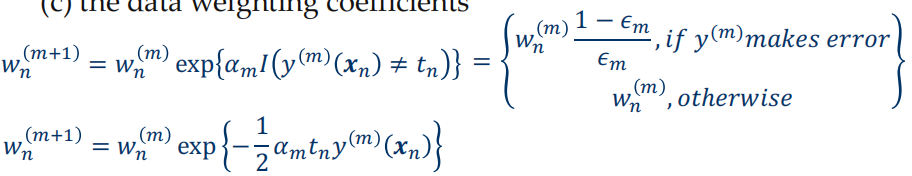
    image-20241111152736194

    • 分析可以得到

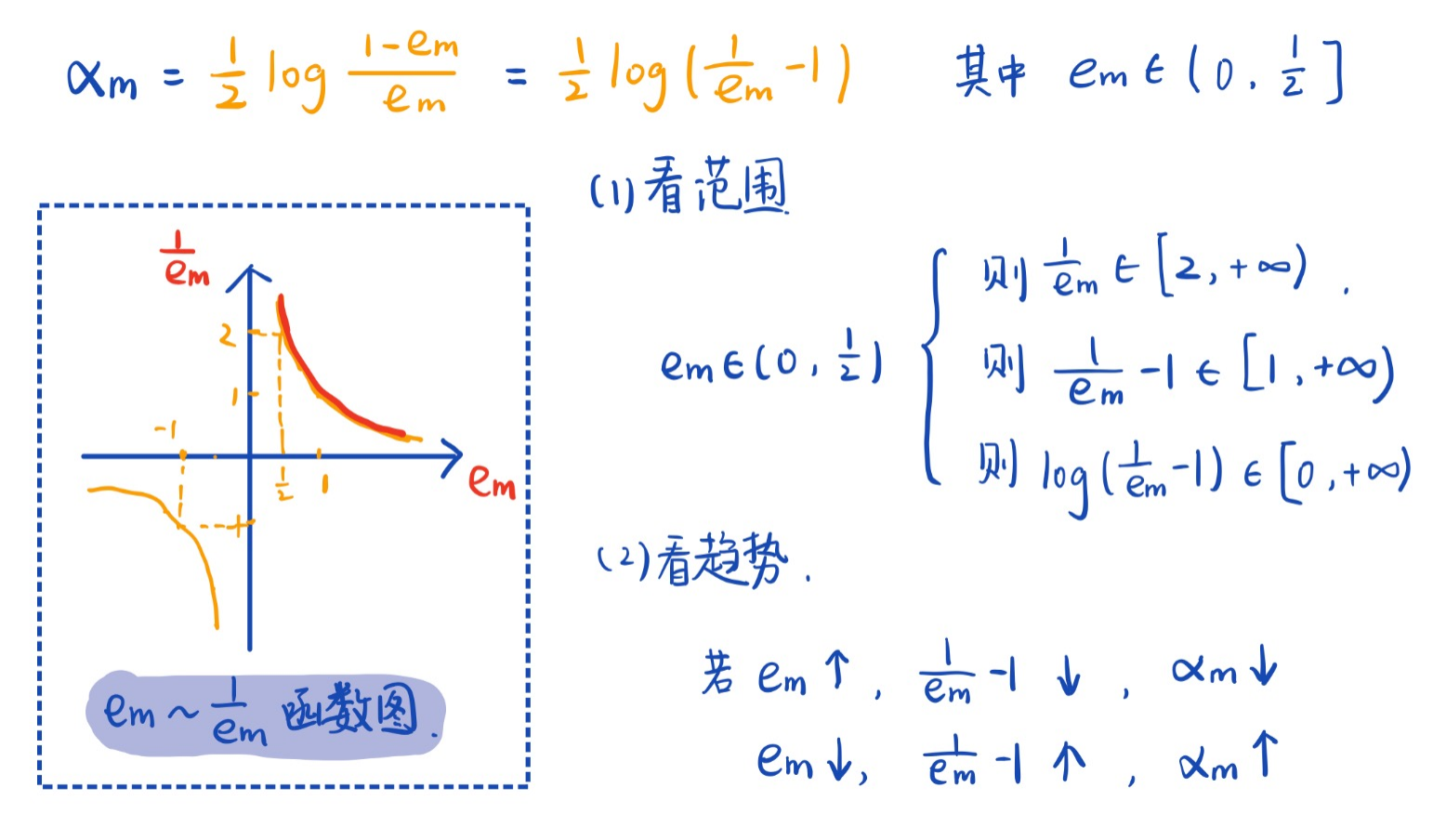
    image-20241111152856446

  2. 使用final model做预测

$$ Y_M(x)=\text{sign}(\sum\limits_{m=1}^M\alpha_my^{(m)}(x)) $$

weighting coefficients \(\alpha_m\) give greater weight to the more accurate classifiers when computing the overall output

Proof

image-20241111153502201image-20241111153527646image-20241111153546309

  1. Optimization

    • exponential error function: $$ E=\sum^N_{n=1}\exp{-t_nf_m(x_n)} $$

      image-20241118012818016

      \[ \begin{aligned} &=\sum_{n=1}^{N}\exp\left\{-t_{n}f_{m-1}(x_{n})-\frac{1}{2}t_{n}\alpha_{m}y_{m}(x_{n})\right\} \newline &=\sum_{n=1}^{N}\exp\{-t_{n}f_{m-1}(\boldsymbol{x}_{n})\}\exp\left\{-\frac{1}{2}t_{n}\alpha_{m}y_{m}(\boldsymbol{x}_{n})\right\} \newline &=\sum_{n=1}^Nw_n^{(m)}\exp\left\{-\frac{1}{2}t_n\alpha_my_m(x_n)\right\} \newline &w_{n}^{(m+1)}=w_{n}^{(m)}\exp\left\{-\frac{1}{2}t_{n}\alpha_{m}y_{m}(x_{n})\right\} \end{aligned} \]

Summary

  • Boosting is sequential ensemble methods, where the base learners are generated sequentially.
  • Bagging is parallel ensemble methods: where the base learners are generated in parallel.
  • Boosting exploit the dependence between the base learners, since the overall performance can be boosted in a residual-decreasing way.
  • Bagging exploit the independence between the base learners, since the error can be reduced dramatically by combining independent base learners.

Gradient Boosting Decision Tree

  1. algorithm
    • 初始化 \(f_0(x)=0\)
    • For m=1,2,...,M
      • Compute the residual: \(r_{mi}=y_i-f_{m-1}(x_i)\)
      • treat \(r_{mi}\) as \(y_i\), learn a regression tree \(h_m(x)\)
      • update \(f_m(x)=f_{m-1}(x)+h_m(x)\)
    • Get the final model \(f_M(x)=\sum\limits_{m=1}^Mh_m(x)\)

Example: A man who is 30. We want to learn a model to fit his age. We use addictive model. The first model we learnt can only predict 20; then we learn another model to fit the remaining 10 and we get a model can predict 6; then we learn another model to fit 4… The final model will be the summation of all models.

评论