5 Kernel Methods

1. generalized linear discriminant function

2. 核方法：对非线性问题，把样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

   • 映射函数 phi-function: \(x\rightarrow\phi(x)\)
   • 对应模型可表示为: \(f(x)=w^\mathrm{T}\phi(x)+b\)
   • 类似有：

   $$ \begin{aligned}&\min_{\boldsymbol{w},b} \frac{1}{2} |\boldsymbol{w}|^{2}\newline &\mathrm{s.t.} y_{i}(\boldsymbol{w}^{\mathrm{T}}\phi(\boldsymbol{x}_{i})+b)\geqslant1,\quad i=1,2,\ldots,m.\end{aligned} $$

   • 对偶问题是

     \[ \begin{aligned} \max_{\alpha}\quad&\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2} \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}\phi(\boldsymbol{x}_{i})^{\mathrm{T}}\phi(\boldsymbol{x}_{j}) \newline \mathrm{s.t.}&\sum_{i=1}^{m}\alpha_{i}y_{i}=0 ,\newline &\alpha_{i}\geqslant0 ,\quad i=1,2,\ldots,m .\end{aligned} \]

   • 求解上式可能比较复杂，可以设想

   $$ \kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=\langle\phi(\boldsymbol{x}_i),\phi(\boldsymbol{x}_j)\rangle=\phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x}_j) $$

   • 即\(x_i\)与\(x_j\)在特征空间的内积等于它们在原始样本空间中通过函数\(\kappa(\cdot,\cdot)\)计算的结果(称为kernel trick)，有了这样的函数。我们就不必直接去计算高维其至无穷维特征空间中的内积，重写为

     \[ \begin{aligned} \max_{\alpha}&\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2} \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}\kappa(\boldsymbol{x}_{i},\boldsymbol{x}_{j})\newline &\mathrm{s.t.}\sum_{i=1}^{m}\alpha_{i}y_{i}=0 ,\newline &\alpha_{i}\geqslant0 ,\quad i=1,2,\ldots,m . \end{aligned} \]

   • 求解后即可得到

   $$ \begin{aligned} f(\boldsymbol{x})& =\boldsymbol{w}^{\mathrm{T}}\phi(\boldsymbol{x})+b \newline &=\sum_{i=1}^{m}\alpha_{i}y_{i}\phi(x_{i})^{\mathrm{T}}\phi(x)+b \newline &=\sum_{i=1}^{m}\alpha_{i}y_{i}\kappa(\boldsymbol{x},\boldsymbol{x}_{i})+b . \end{aligned} $$

3. 核函数：令\(\mathcal{X}\)为输入空间，\(\kappa(\cdot,\cdot)\)是定义在\(\mathcal{X}\times\mathcal{X}\)上的对称函数，则\(\kappa\)是核函数当且仅当对于任意数据\(D=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_m\}\),“核矩阵”(kernel matrix) K 总是半正定的：

$$ \begin{gathered}\mathbf{K}=\begin{bmatrix}\kappa(\boldsymbol{x}_1,\boldsymbol{x}_1)&\cdots&\kappa(\boldsymbol{x}_1,\boldsymbol{x}_j)&\cdots&\kappa(\boldsymbol{x}_1,\boldsymbol{x}_m)\newline \vdots&\ddots&\vdots&\ddots&\vdots\newline \kappa(\boldsymbol{x}_i,\boldsymbol{x}_1)&\cdots&\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)&\cdots&\kappa(\boldsymbol{x}_i,\boldsymbol{x}_m)\newline \vdots&\ddots&\vdots&\ddots&\vdots\newline \kappa(\boldsymbol{x}_m,\boldsymbol{x}_1)&\cdots&\kappa(\boldsymbol{x}_m,\boldsymbol{x}_j)&\cdots&\kappa(\boldsymbol{x}_m,\boldsymbol{x}_m)\end{bmatrix}.\end{gathered} $$

4. dual representations: Ridge Regression

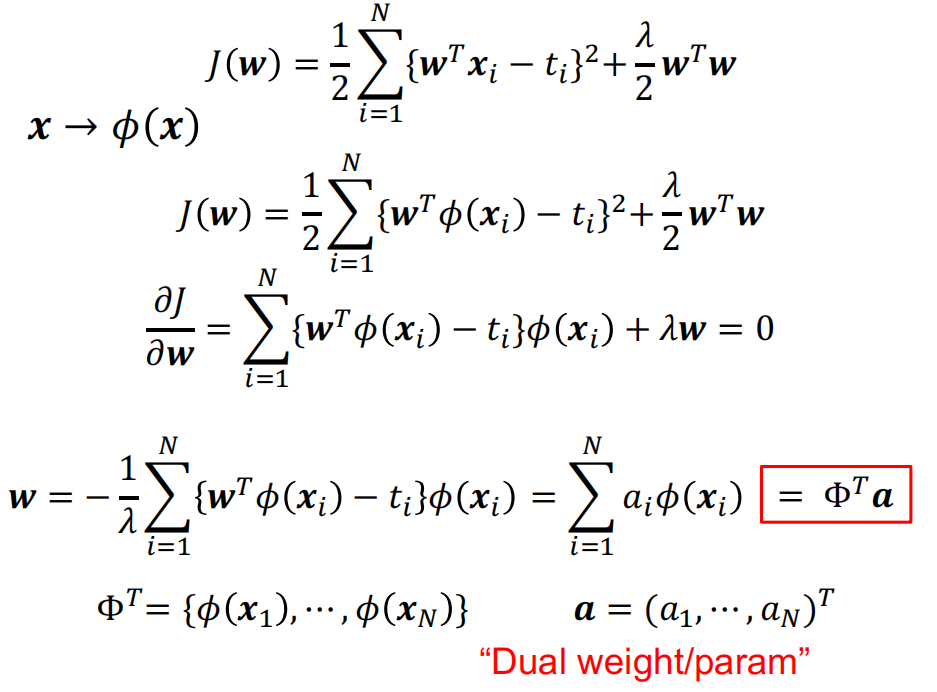
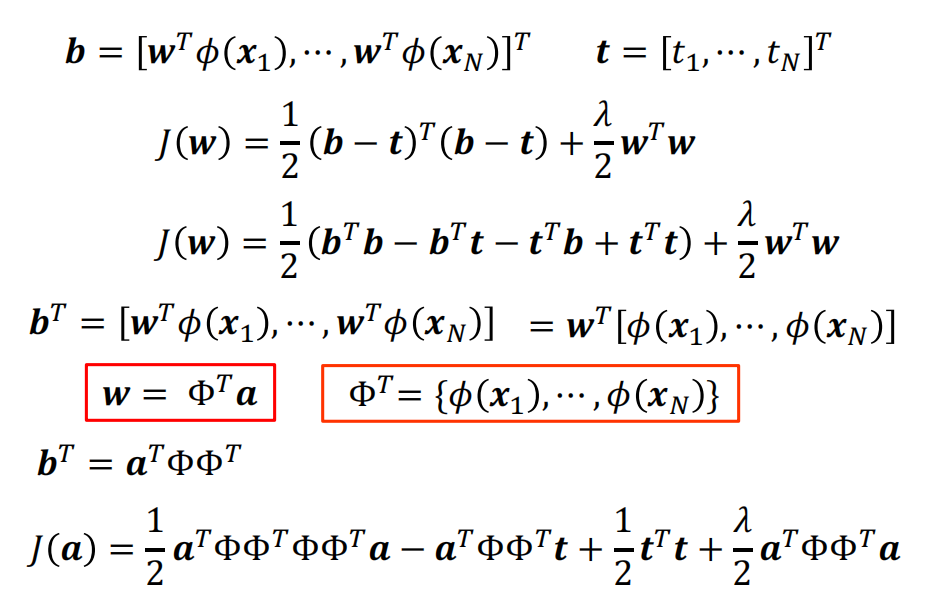
$$ \text{Define Gram matrix} K=\Phi\Phi^T \newline \Phi^{T}={\phi(x_1),\cdots,\phi(x_N)}\newline K_{nm}=\phi(x_n)^T\phi(x_m)=k(x_n,x_m)\newline k(x,x^{\prime})\to\phi(x)^T\phi(x^{\prime}) $$

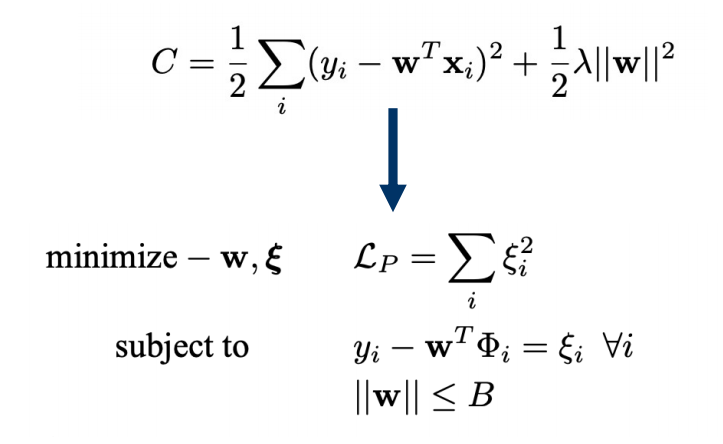
5. Maximum Margin Classifier

   
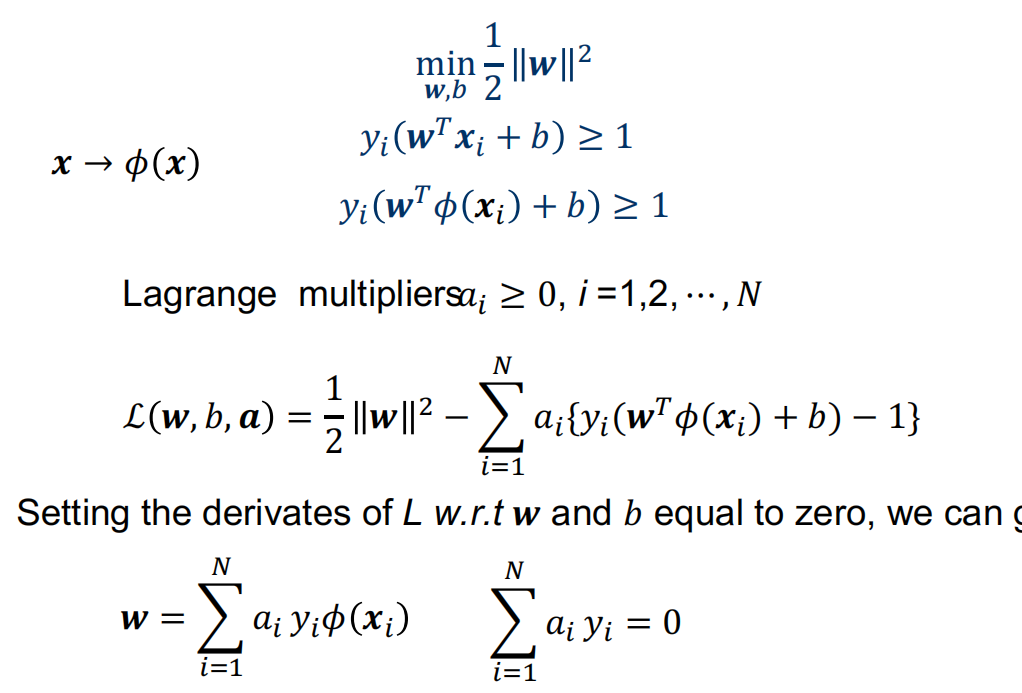
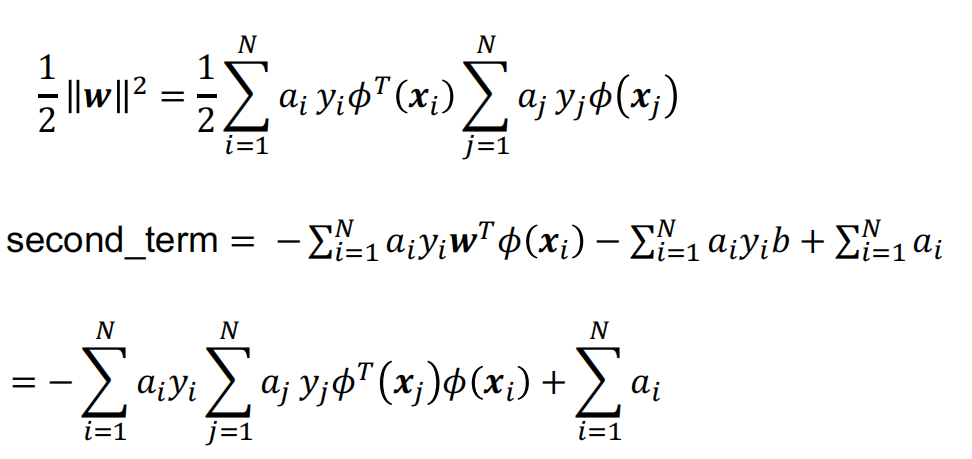   \[ \begin{aligned} \mathcal{L}(\boldsymbol{a})=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}&a_{i}a_{j}y_{i}y_{j}\phi^{T}(\boldsymbol{x}_{i})\phi(\boldsymbol{x}_{j})+\sum_{i=1}^{N}a_{i}\newline \mathcal{L}(\boldsymbol{a})=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}&a_{i}a_{j}y_{i}y_{j}k(\boldsymbol{x}_{i},\boldsymbol{x}_{j})+\sum_{i=1}^{N}a_{i}\newline a_{i}\geq0&\quad \sum_{i=1}^{N}a_{i}y_{i}=0 \newline f(\boldsymbol{x})=\boldsymbol{w}^T\phi(\boldsymbol{x})+b&\quad \boldsymbol{w}=\sum_{i=1}^Na_iy_i\phi(\boldsymbol{x}_i)\newline f(\boldsymbol{x})=\sum_{i=1}^Na_iy_i\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x})&+b=\sum_{i=1}^Na_iy_ik(\boldsymbol{x}_i,\boldsymbol{x})+b \end{aligned} \]

6. 常用核函数

   • Polynomial kernels $$ k(x,x')=(x^Tx'+1)^d $$
   
   • 核函数之间也可以线性组合、直积等等

7. 当训练实例的数量小于特征数量时，解决对偶问题比原始问题更迅速

评论