2 Linear Regression¶
-
mean-squared error(MSE): \(J_n=\dfrac{1}{n}\sum\limits_{i=1}^n(y_i-f(x_i))^2\)
-
residual sum of squares: \(RSS(f)=\sum\limits_{i=1}^n(y_i-f(x_i))^2\)
-
for matrix: \(J_n(w)=(y-X^Tw)^T(y-X^Tw)\)
-
Maximum Likelihood Estimation:
- Likelihood of predictions: The probability of observing outputs \(y\) in \(D\) given \(w,X,\) and \(\sigma\)
-
\(L(D,w,\sigma)=\prod\limits_{i=1}^np(y_i|x_i,w,\sigma)\)
-
\(w^*=\operatorname{argmax}\prod\limits_{i=1}^np(y_i|x_i,w,\sigma)\)
-
Over-fitting
- 解 \(w=(XX^T)^{-1}Xy\)
- 若 \(XX^T\) 非奇异(满秩),则有唯一解,否则会导致过拟合
-
Ridge Regression 二阶正则项
- control the size of the coefficients in Regression
- local smoothness
- weight decay
$$ w^*=\operatorname{argmin}\sum_{i=1}^n\left(y_i-x_i^Tw\right)^2+\lambda\sum_{j=1}^pw_j^2 $$
- equivalent formulation
$$ \boldsymbol{a}^*=\operatorname{argmin}\sum_{i=1}^n\left(y_i-x_i^T\boldsymbol{w}\right)^2 \ \text{Subject to} \Sigma_{j=1}^pw_j^2\leq t $$
推导

- control the size of the coefficients in Regression
-
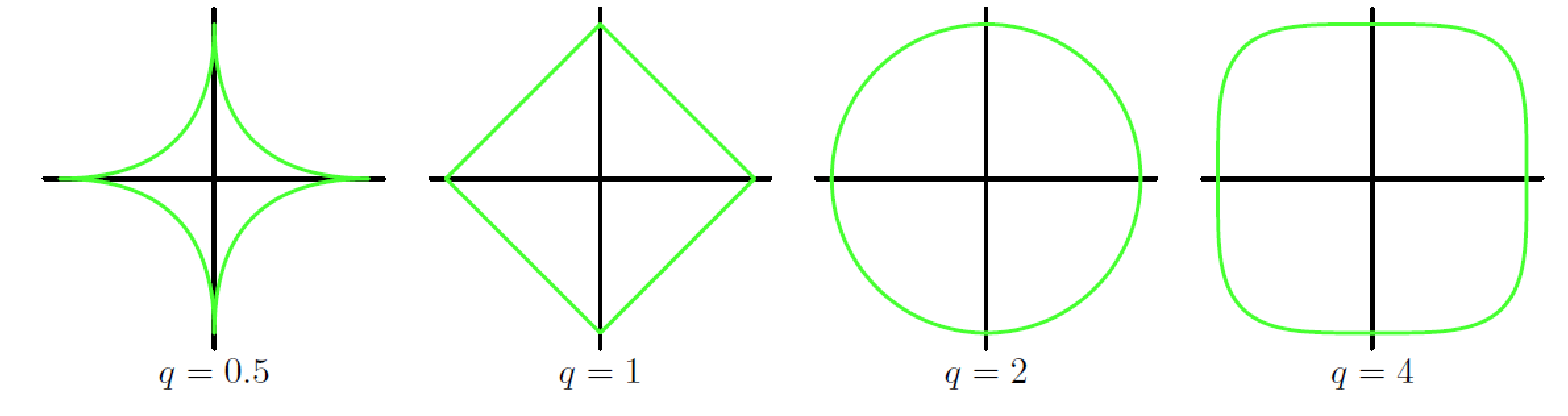
subject to \(\sum\limits_{j=1}^p|w_j|^q\leq t\)
-
LASSO(Least Absolute Selection and Shrinkage Operator)
\[ \widehat{\boldsymbol{w}}=\operatorname{argmin}\frac{1}{2n}\sum_{i=1}^{n}\left(y_{i}-x_{i}^{T}w\right)^{2} \ \ \ \ \ \ \text{subject to}\sum_{j=1}^p|w_j|\leq t\\ or \ \ \ \ \ \ \ \ \widehat{\boldsymbol{w}}=\operatorname{argmin}\frac{1}{2n}\sum_{i=1}^{n}\left(y_{i}-x_{i}^{T}w\right)^{2}+\lambda\|w\|_{1} \]-
sparse model: 如上图q=1所示,更容易取到坐标轴上的角,对应的是有某一坐标分量为0,因此更能提取到重要的特征
-
solution
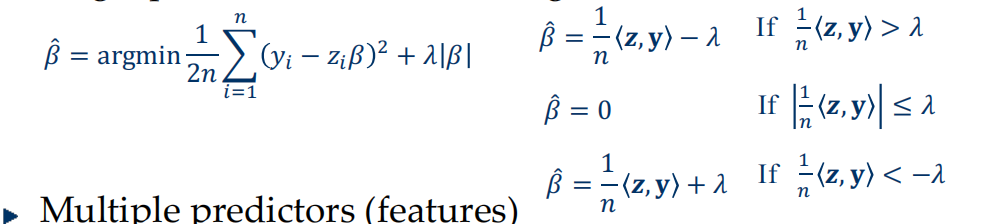
-
-
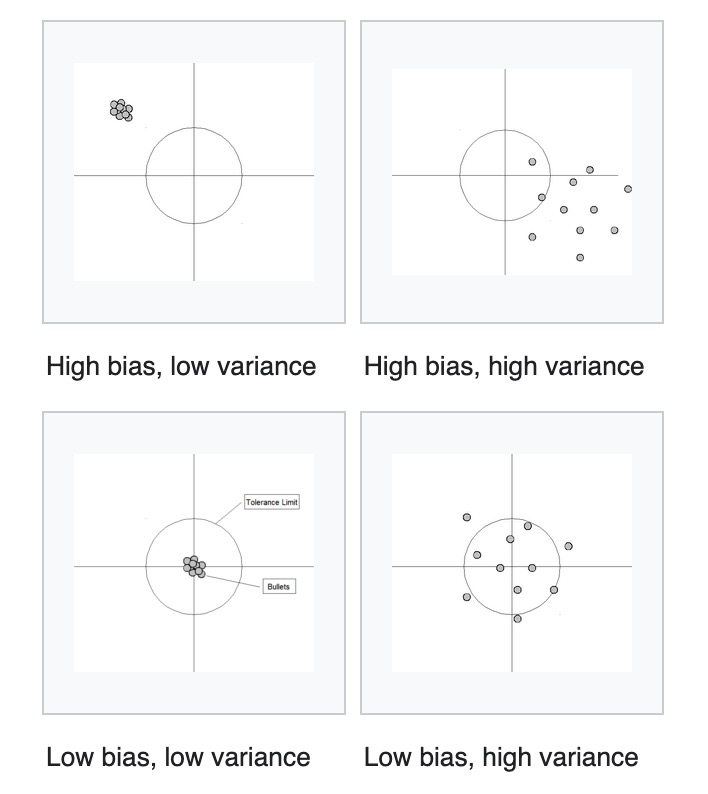
Bias & Variance Decomposition
- Given training set D, so \(f(x)\rightarrow f(x;D)\), and \(E_D(f(x;D))\)


-
expected prediction error = \((\text{bias})^2+\text{variance}+\text{noise}\)
-
(bias\()^2:\) 相当于拟合出来的函数和y的偏差 $$ \int{E_D(f(x;D))-E(y|x)}^2p(x)dx $$
-
variance: 拟合出的函数本身的方差
\[ \int E_D\left\{\left[f(\boldsymbol{x};D)-E_D(f(\boldsymbol{x};D))\right]^2\right\}p(\boldsymbol{x})d\boldsymbol{x} \]- noise:
\[ \int\mathrm{var}(y|x)p(x)dx \] -
-
Cross-Validation:
- K-Fold Cross-Validation
- leave-one-out cross-validation