12 Clustering

Gaussian Mixture Model

可能有缺漏

1. Gaussian Mixture Model (GMM) is one of the most popular clustering methods which can be viewed as a linear combination of different Gaussian components.

   
   • The log-likelihood function
   \[ \log\prod\limits_{i=1}^Np(x^{(i)};\Theta)=\sum_{i=1}^N\log(\sum_{k=1}^K\pi_k\mathcal{N}(x^{(i)};\mu_k,\Sigma_k)) \]
   

   • parameters estimation for GMM

     

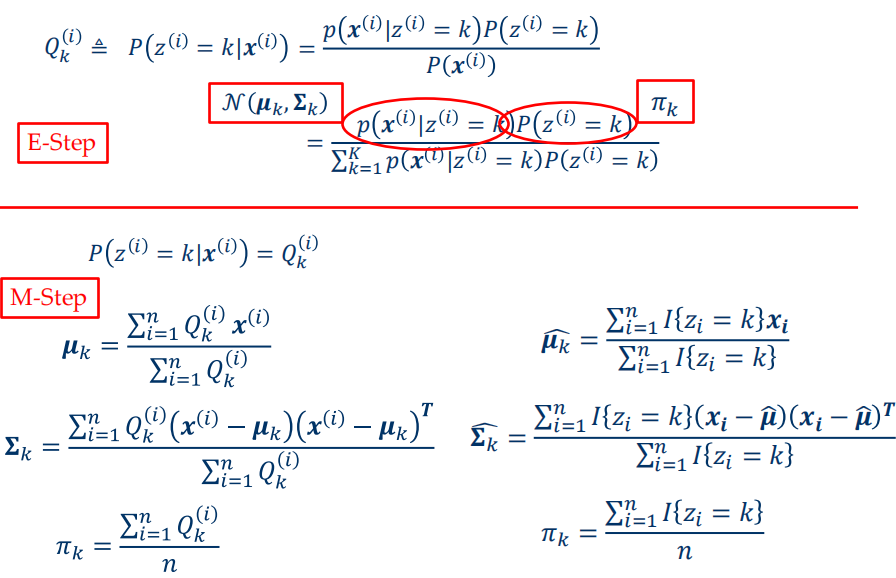
Density-Based Clustering Methods

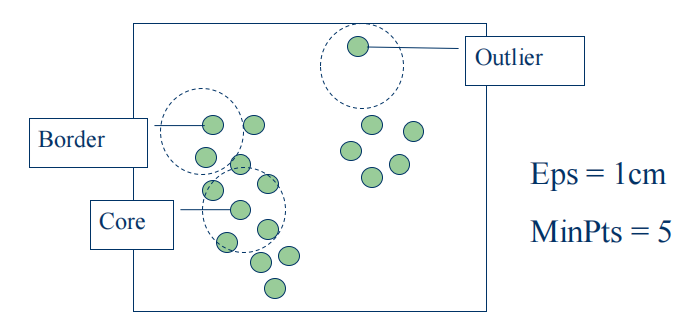
1. two parameters

   • Eps: Maximum radius of the neighborhood
   • MinPts: Minimum number of points in an Eps-neighborhood of that point

2. \(N_{Eps}(p)\):{q belongs to D | \(dist(p,q)\leq Eps\)}

3. Directly density-reachable: A point p is directly density-reachable from a point q if p belongs to \(N_{Eps}(q)\) and \(|N_{Eps}(q)|\geq MinPts\)

   

4. DBSCAN

   • Arbitrary select a point p
   • Retrieve all points density-reachable from p w.r.t. Eps and MinPts
   • If p is a core point, a cluster is formed
   • If p is a border point, no points are density-reachable from p and DBSCAN visits the next point of the database
   • Continue the process until all of the points have been processed

Spectral Clustering

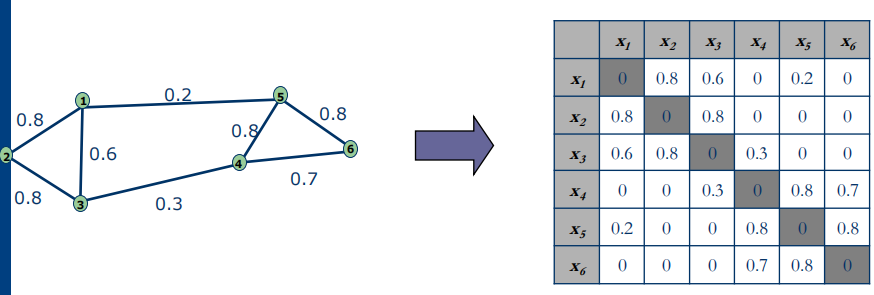
1. Represent data points as the vertices V of a graph G, clustering can be viewed as partitioning a similarity graph. Large weights mean that the adjacent vertices are very similar; small weights imply dissimilarity.

   • Naïve Idea: make the weight of those cut edges as small as possible

2. Cut: Set of edges with only one vertex in a group.

$$ cut(A,B)=\sum_{i\in A.j\in B}w_{ij} $$

3. Association: Set of edges with two vertexes in the same group.

$$ assoc(A,A)=\sum_{i\in A,j\in A}w_{ij} $$

4. Normalized Cut Criteria

$$ \begin{aligned} Ncut(A,B)&=\frac{cut(A,B)}{assoc(A,V)}+\frac{cut(A,B)}{assoc(B,V)} \newline
assoc(A,V)&=\sum_{i\in A, j\in V}w_{ij} \newline
\text{goal:} \quad &\min Ncut(A,B) \end{aligned} $$

5. matrix representation: symmetric matrix 得到\(W\),同时对角阵D，有\(d_i=\sum\limits_jw_{ij}\)

6. objective function

   \[ \begin{aligned} x\in[1,-1]^n,&x_i=\begin{cases}1&i\in A\newline -1&i\in B&\end{cases} \newline y=(1+x)&-b(1-x) \newline \min_y \frac{y^T(D-W)y}{y^TDy},& y\in\mathcal{R}^n,y^TD1=0 \end{aligned} \]
   • make \(L=D-W\), then \(\min\limits_y y^TLy\ \ \ s.t.\ y^TDy=1\)
   • by Lagrangian Function \(Ly=-\lambda Dy\), which is a generalized Eigen-problem
   • change it to \(D^{-1}Ly=\lambda y\)

7. K>2

   • perform Ncut recursively

   • use more than one eigenvectors

     • suppose \(y_1,y_2,\cdots,y_k\) are the first k eigenvectors corresponding to the smallest eigenvalues, let

     \(Y=[y_1,y_2,\dots,y_k]\in R^{n\times k}\)

     • each row vector of \(Y\) is a k dimensional representation of the original data point

     • performing Kmeans

8. Spectral Clustering Algorithm

   1. Graph construction
      • Heat kernel \(w_{ij}=\exp\{-\dfrac{\|x_i-x_j\|}{2\sigma^2}\}\)
      • k-nearest neighbor graph
   2. Eigen-problem
      • Compute eigenvalues and eigenvectors of the matrix L
      • Map each point to a lower-dimensional representation based on one or more eigenvectors.
   3. Conventional clustering schemes, e.g. K-Means
      • Assign points to two or more clusters, based on the new representation.

LVQ

评论