10 kNN & Metric

k Nearest Neighbor Classifier

1. requires three things
   • the set of stored records
   • distance metric to compute distance between records
   • the value of \(k\)

2. To classify an unknown record:

   • Compute distance to other training records
   • Identify \(k\) nearest neighbors
   • Use class labels of nearest neighbors to determine the class label of unknown record (e.g., by taking majority vote)

3. Metric Learning: 在距离衡量中加入权重，考虑不同feature的重要性

   \[ \rho_M(x,y)=\sqrt{(x-y)^TM(x-y)} \]
   • 我们希望对同类距离尽可能小，异类尽可能大
   • Create cost/energy function and minimize with respect to M $$ \mathcal{L}(M)=\sum_{(x,x^{\prime})\in S}\rho_{M}^{2}(x,x^{\prime})-\lambda\sum_{(x,x^{\prime})\in D}\rho_{M}^{2}(x,x^{\prime}) $$

4. MMC (Mahalanobis Metric for Clustering)

   
   • 取对数
   

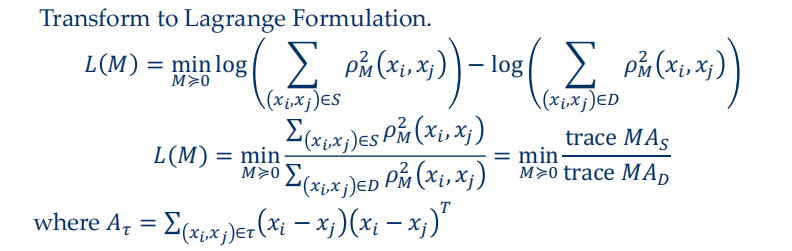
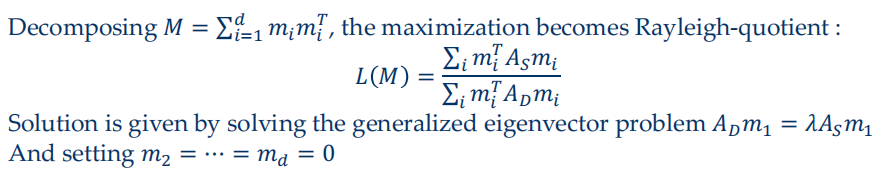
AKNN Search

• Given a dataset D contains n d-dim data points, find nearest neighbor: \(O(nd+n)\)
  • find k: \(O(nd+kn)\) or \(O(nd+k\log n )\) or \(O(nd+n\log k)\)

• \(\epsilon\)-approximate nearest neighbor search

• method for ANNS:

  • partition the space
    • tree based
    • graph based
  • approximation
    • hashing based
    • Quantization based

• K-D Tree

  • 假设我们已经知道了 k 维空间内的 n个不同的点的坐标，要将其构建成一棵 k-D Tree，步骤如下：
    1. 若当前超长方体中只有一个点，返回这个点。
    2. 选择一个维度，将当前超长方体按照这个维度分成两个超长方体。
    3. 选择切割点：在选择的维度上选择一个点，这一维度上的值小于这个点的归入一个超长方体（左子树），其余的归入另一个超长方体（右子树）。
    4. 将选择的点作为这棵子树的根节点，递归对分出的两个超长方体构建左右子树，维护子树的信息。
  • 提出两个优化：
    1. 轮流选择 k 个维度，以保证在任意连续 k 层里每个维度都被切割到。
    2. 每次在维度上选择切割点时选择该维度上的 中位数，这样可以保证每次分成的左右子树大小尽量相等。
  • 优化后高度最多 \(\log n+O(1)\)
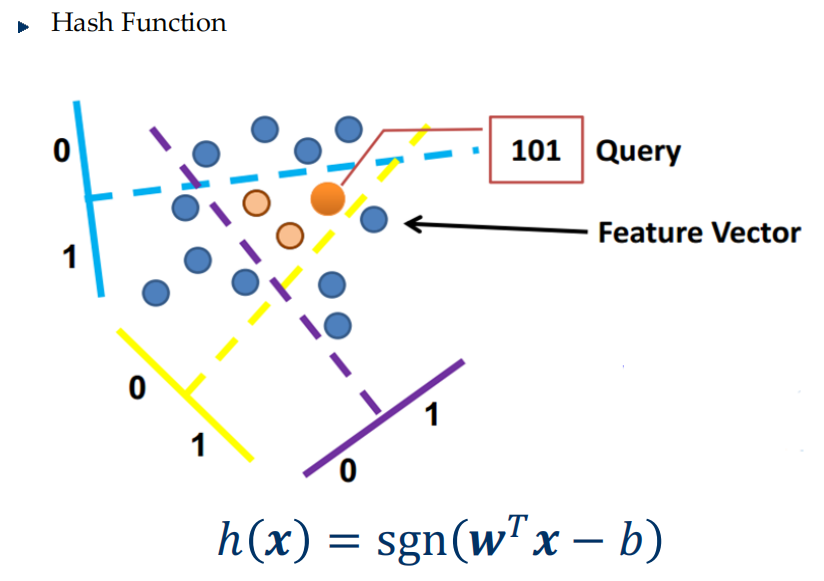
• Locality Sensitive Hashing (LSH)
  • Basic assumption: Similar data (in certain dimensions) is likely to be thrown into the same bucket.
  • While querying, the same set of hashing functions will be used.
  • The hashing functions can be randomized or designed.
  • Often times, built upon extracted features.
  • LSH generates bunch of candidate points, followed by other post-processing mechanisms.

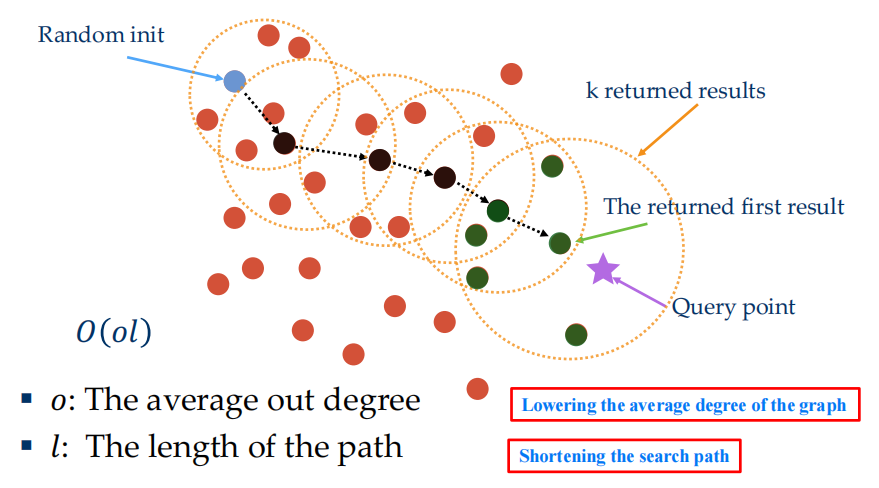
• Graph based ANNS algorithms
  • Motivation: Neighbor’s neighbor is also likely the neighbor.
  • Appealing theoretical properties on search but huge indexing time complexity (at least \(O(n^2)\))

评论