跳转至

9 MARL with A-C

MADDPG

  1. 传统算法在多智能体环境中：对单个智能体，环境不稳定，状态转移矩阵不同，不能直接经验回放，方差问题加剧。

  2. MADDPG:

    • 学习到的策略可以分布式执行，即智能体根据自己的观察结果来决策；
    • 不需要假定环境动态系统是可微的，也不需要假设智能体之间的通讯方式有任何特性结构，即世界模型和通信模型都不要求是可微的；
    • 因为每个智能体最大化各自的累积奖励，MADDPG不仅可应用于具有明确通信渠道的合作博弈，还可以应用于竞争博弈。

  3. MAAC架构

    • 针对智能体i的策略梯度公式

      \[ \nabla_{\theta_i}J(\theta_i)=\mathbb{E}_{s\sim p^\pi,a\sim\pi_\theta}[\nabla_{\theta_i}log\pi_i(a_i|o_i)Q_i^\pi(x,a_1,...a_N)] \]

    • \(Q^\pi_i(x,a_1,\dots,a_N)\)是一个集中的动作价值函数，输入为所有智能体的动作和一些状态信息，输出每个智能体的动作价值

    • x包含所有智能体的观测信息以及通信信息等额外信息

  4. MADDPG算法基于以下原理：

    • 每个智能体输出确定性动作，即

      \[ P(s'|a_1,...a_N,\pi_1,...\pi_N)=P(s'|a_1,...a_N)=P(s'|a_1,...a_N,\pi_1',...\pi_N'),\quad\pi_i'\neq\pi_i \]

    • 即不论策略是否相同，只要产生的动作相同，就可以认为状态转移不变

    • 这样只要已知各个智能体的动作，即便生成的策略不同，环境依旧是稳定的

  5. 算法：

    • 经验回放缓存，交互数据存入\(\mathcal{D}\)，如下训练

      \[ \begin{gathered} \nabla_{\theta_i}J(\mu_i)=\mathbb{E}_{x,a\sim D}[\nabla_{\theta_i}\mu_i(a_i|o_i)\nabla_{a_i}Q_i^\mu(x,a_1,...a_N)| a_i=\mu_i(o_i)] \end{gathered} \]

    • 其中全局中心化的\(Q_i^\mu\)如下更新：

      \[ \begin{gathered} L(\theta_{i})=\mathbb{E}_{x,a,r,x^{\prime}}[(Q_{i}^{\mu}(x,a_{1},...,a_{N})-y)^{2}]\\y=r_{i}+\gamma Q_{i}^{\mu^{\prime}}(x^{\prime},a_{1}^{\prime},...a_{N}^{\prime})|a_{j}^{\prime}=\mu_{j}^{\prime}(o_{j}) \end{gathered} \]

    • 每个智能体i维护一个对智能体j策略的近似\(\hat{\mu}_{\phi_i^j}\)​的对手网络智能体𝑗的真实策略为\(\mu_j\)，该策略可以通过智能体𝑗行为对数概率以及熵正则的方式进行学习

      \[ \begin{gathered} L(\phi_{i}^{j})=-\mathbb{E}_{o_{j},a_{j}}[log\hat{\mu}_{i}^{j}(a_{j}|o_{j})+\lambda H(\hat{\mu}_{i}^{j})]\\\hat{y}=r_{i}+\gamma Q_{i}^{\mu^{\prime}}(x^{\prime},\hat{\mu}_{i}^{\prime1}(o_{1}),...,\hat{\mu}_{i}^{\prime N}(o_{N})) \end{gathered} \]

    • 其中H为熵，\(\hat{\mu}_i^{'j}\)为目标网络

image-20240711100007662

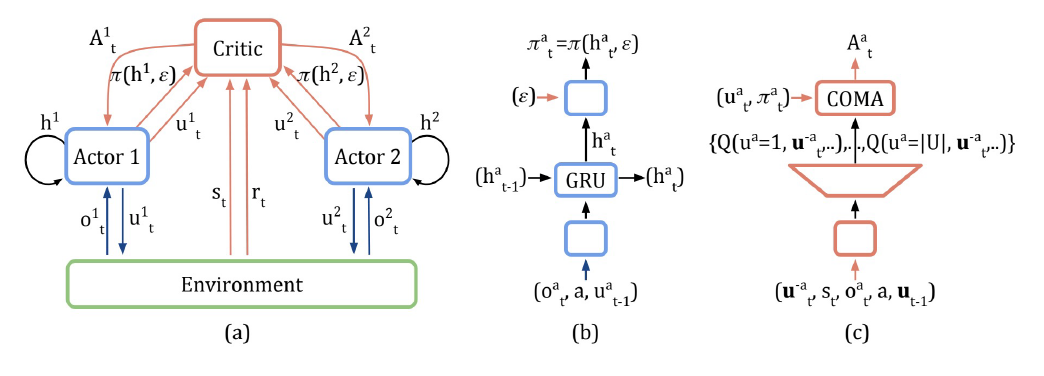
COMA

  1. 用于学习非中心式的、部分可观测的多智能体协同的控制策略

  2. 采用反事实基线（counterfactual baseline）来解决信用分配的问题；为了应对多智能体信用分配的挑战，COMA使用了一个反事实基线将单个智能体的行动边缘化，而其他智能体的行动保持不变。“如果智能体不采用当前的行为，那会不会有更多的收益”；

  3. 反事实基线可由:\(D_i=r(s,a)-r(s,(a_{-i},c_i))\)，其中\(D_i\)为智能体i的独立行为回报，\(c_i\)为基线默认行为

  4. 使用Critic网络计算\(D_i\)的值，取所有行为的均值作为默认行为的效用值

\[ \begin{gathered}Q(s,c_{i})=\sum_{a_{i}'}\pi_{i}(a_{i}'|\tau_{i})Q(s,(a_{-i},a_{i}'))\\A_{i}(s,a)=Q(s,a)-\sum_{a_{i}'}\pi_{i}(a_{i}'|\tau_{i})Q(s,(a_{-i},a_{i}')) \end{gathered} \]
  1. 维度诅咒：\(A^N\)计算消耗太大
image-20240711101003739image-20240711101136504

  1. V.S. MADDPG：

    • COMA针对离散动作，学习的是随机策略。而MADDPG针对连续动作，学习的是确定性策略。这在它们策略梯度函数的表达式上能够体现出区别。
    • COMA主要针对多智能体协作任务，因此只有一个critic评价团队整体的回报。MADDPG既可以做协作任务，也可以做竞争任务，每个智能体都对应一个奖励函数，因此每个智能体对应一个critic。
    • COMA使用了历史观测、动作序列作为网络的输入，而MADDPG没有使用历史序列。因此COMA的网络结构中包含了GRU层，而MADDPG的网络均为2-3个隐层的MLP。
    • COMA中所有智能体的actor网络共享参数，输入端加上智能体ID以示区别。而MADDPG则没有共享参数；
    • COMA使用反事实基线作为actor网络的优化目标，而MADDPG直接使用Q函数作为每个智能体actor网路的优化目标。

  2. 优缺点：

    • 采用AC架构，易于并行化，训练起时间比较快；
    • 真实表现相对低迷，是AC领域算法的baseline；
    • 使用时易于实现，增加实现技巧可以有表现提升

LICA

  1. LICA值分解算法无需满足IGM约束，LICA将值分解迁移到AC算法框架后，因为Actor是使用来自Critic的梯度更新的，所以基于局部Actor选出来的最优动作也必然是全局Critic的最优动作
  2. LICA的Critic使用了超网络，将动作输入到Critic网络，其MLP 的权重则由基于当前全局状态的超网络确定，此时全局状态和动作实际上属于相乘关系，求动作的偏导时梯度中会包含当前全局状态的信息，从而更准确地计算各智能体具体信用。
\[ \frac{\partial Q_\phi^\pi}{\partial u}=\frac{\partial Q_\phi^\pi}{\partial v}\frac{\partial v}{\partial u} ,with v=\begin{cases}\\f_s(s)+f_u(u)\\f_s(s)f_u(u)\end{cases},and \frac{\partial v}{\partial u}=\frac{\partial v}{\partial f_u}\frac{\partial f_u}{\partial u}=\begin{cases}\frac{\partial f_u}{\partial u},&\quad for MLP\\f_s(s)\frac{\partial f_u}{\partial u},&\quad for MIX\end{cases} \]
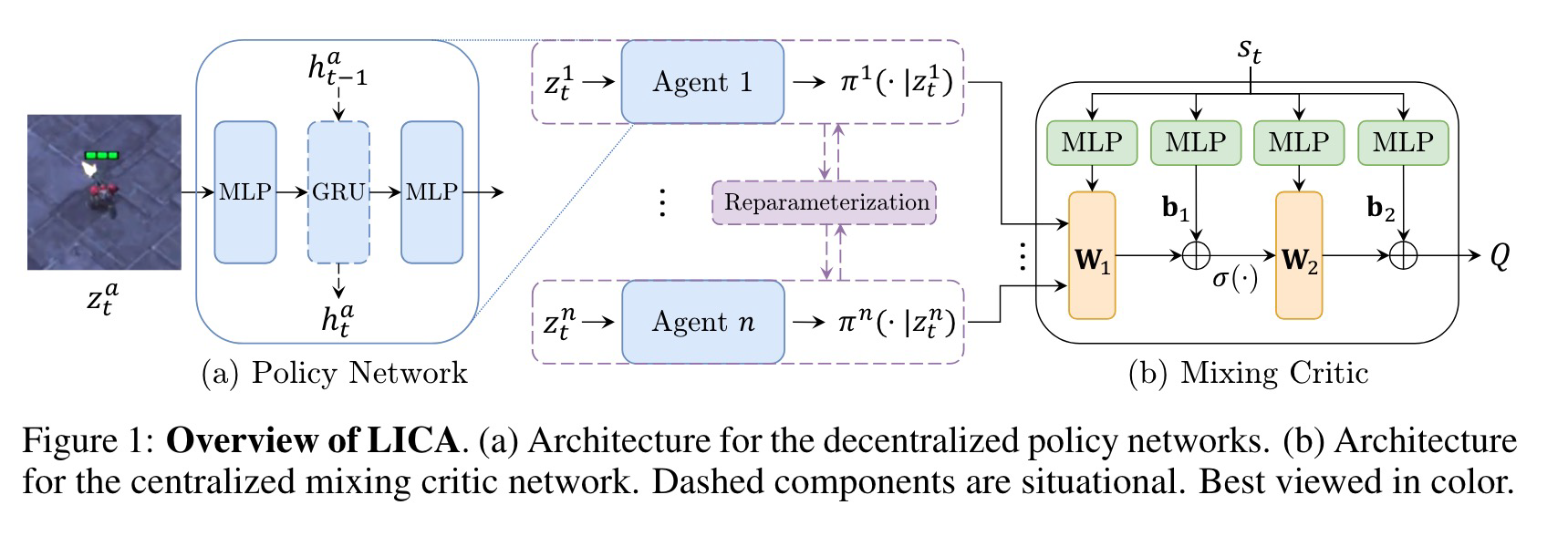
image-20240711102056171
  1. 对于Critic部分，LICA采用了GAE和\(TD(\lambda)\)的变体，其更新为：
\[ \begin{gathered} \mathcal{L}(\phi)=\min_{\phi}\mathbb{E}_{\tau\sim\pi_{\theta}(\tau)}\left[\left(y_{t}^{(\lambda)}-Q_{\phi}^{\pi}(s_{t},u_{t})\right)^{2}\right]\\y_{t}^{(\lambda)}=r_{t}+\gamma(\lambda y_{t+1}^{(\lambda)}+(1-\lambda)Q_{\phi}^{\pi}(s_{t+1},u_{t+1})) \end{gathered} \]
  1. 更新Actor引入了熵项
\[ \begin{gathered} J(\theta)=\mathbb{E}_{\tau\sim\pi_{\theta}(\tau)}\left[Q_{\phi}^{\pi}(s_{t},u_{t})+\mathbb{E}_{a}\left[\mathcal{H}\left(\pi_{\theta_{a}}^{a}(.|z_{t}^{a})\right)\right]\right] \\ \frac{\partial J(\theta_a)}{\partial\theta_a}\approx\mathbb{E}_{\tau\sim\pi_\theta(\tau)}\left[\frac{\partial Q_\phi^\pi(s_t,\pi_t^1,...\pi_t^n)}{\partial\pi_t^a}\frac{\partial\pi_t^a}{\partial\theta_a}+\frac{\partial\mathcal{H}(\pi_t^a)}{\partial\theta_a}\right] \\ \mathcal{H}\big(\pi^{a}(.|z^{a})\big)=\beta H\big(\pi^{a}(.|z^{a})\big)=\beta\mathbb{E}_{u^{a}\thicksim\pi^{a}}[-log\pi^{a}(u^{a}|z^{a})] \end{gathered} \]

  1. 引入超参数\(\beta\)，假设智能体a的某个动作概率为p，对熵求导 $$ \begin{gathered} p^a=\pi^a(.|z^a)\ d\mathcal{H}=\left[\frac{\partial\mathcal{H}}{\partial p_1^a},...,\frac{\partial\mathcal{H}}{\partial p_k^a}\right]=[-\beta(logp_1^a+1),...,-\beta(logp_k^a+1)] \end{gathered} $$

  2. 当选择某个动作概率较大时，熵项的约束较小；而当选择某个动作概率较小时，熵项的约束反而较大。

\[ d\mathcal{H}_i:=-\xi.\frac{logp_i^a+1}{H(p_a)} \]

MAPPO

  1. 发现使用价值归一化从不会对训练产生负面影响，并且通常能显著提升MAPPO 的最终性能

  2. MAPPO价值函数的输入

    • CL：所有本地观测的串联(concatenation of local observations, CL)形成的全局状态。
    • EP：采用了一个包含环境状态概况信息的环境提供的全局状态(Environment-Provided global state, EP)
    • AS(EP+特定agent的观测)：特定智能体的全局状态(Agent-Specific Global State, AS)，它通过连接EP状态和\(o_i\)为智能体\(i\)创建全局状态。这为价值函数提供了对环境状态的更全面描述。
    • FP：为了评估这种增加的维度对性能的影响，MAPPO通过移除AS状态中重复的特征，创建了一个特征剪枝的特定智能体全局状态(Featured-Pruned Agent-Specific Global State, FP)。

  3. 训练数据利用

    • PPO 的一个重点特性是使用重要性采样（importance sampling）进行非策略（off-policy）校正，这允许重复使用样本数据。也就是将收集的大量样本分成小批次，并进行多个训练周期（epochs）的训练。
    • 在单智能体连续控制领域，常见做法是将大量样本分成大约32或64个小批次，并进行数十个训练周期。然而，在多智能体领域，我们发现当样本被过度重用时，MAPPO 的性能会降低（也就是不能重复使用次数太多）。
    • 这可能是由于多智能体强化学习中的非平稳性（non-stationarity）：减少每次更新的训练周期数可以限制智能体策略的变化，这可能有助于提高策略和价值学习的稳定性。

  4. MAPPO-Clip

    • PPO 的另一个核心特征是利用剪切的重要性比例（clipped importanceratio）和价值损失（value loss），以防止策略和价值函数在迭代过程中发生剧烈变化。剪切的强度由超参数ϵ控制：较大的ϵ值允许对策略和价值函数进行更大的更新。
    • 与训练周期数类似，假设策略和价值的剪切可以限制由于智能体策略在训练中的变化而引起的非平稳性。对于较小的ϵ，智能体的策略在每次更新中的变化可能会更小，因此可以在可能牺牲学习速度的情况下，提高整体学习的稳定性。

  5. Batchsize：为了获得MAPPO 的最佳任务性能，请使用较大的批次大小。然后，调整批次大小以优化样本效率

image-20240711103812368

评论