跳转至

7 MARL with Factored Value Functions

博弈论概念

  1. 回报payoff, utility \(u=(u_1,u_2,\dots,u_n)\rightarrow\mathbb{R}\)
    • \(u_1: A_1\times A_2\rightarrow\mathbb{R}\)
  2. 回报矩阵
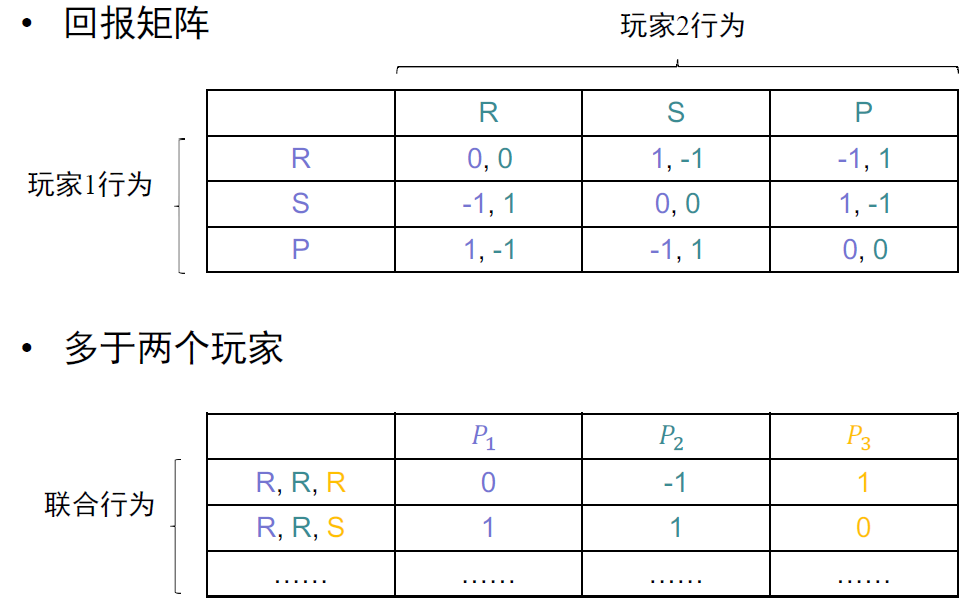
image-20240709095318590

  1. 共识：A和B同时被告知游戏规则

  2. 纯策略与混合策略

image-20240709095537051
  1. 最佳策略博弈
    • 给定\(a_{-i}\in A_1\times A_2\times\cdots\times A_{i-1}\times A_{i+1}\times\cdots\times A_n\)
    • 如果\(\forall a_i'\in A_i,u_i(a_i,a_{-i})\geq u_i(a_i',a_{-i})\)，则\(a_i\)是针对\(a_{-i}\)的最佳策略
  2. 占优策略(dominant strategy)
    • 给定\(\forall a_{-i},a_i\)都是最佳策略博弈，则为占优策略
  3. 纳什均衡/混合策略纳什均衡：联合策略为纳什均衡解，当且仅当对每个玩家，策略\(a_i\)都是最佳博弈

多智能体信用分配

  1. MA-MDP模型假设：每个智能体都可以获取全局状态

  2. Dec-POMDP：智能体无法获得全局状态，只能看到全局状态的投影

    • 观测：\(o_i\in\Omega\)
    • 观测函数：\(o_i\in\Omega\sim O(s,i)\)
    • 智能体i的分布式策略：\(\pi_i(\tau_i):T\rightarrow A\)
      • 行为观测历史：\(\tau_i\in T=(\Omega\times A)^*\)
    • 集中训练分布式执行(CTDE)
      • 训练过程可以获取全局状态
      • 测试过程只能看到局部观测

  3. MARL挑战

    • 可扩展性：维度诅咒
    • 多智能体信用分配：每个智能体对整体博弈的贡献
    • 样本利用率：需要大量的交互数据
    • 受限的观测：受限传感器，无法获取全局信息
    • 探索：指数级别的联合策略空间

MARL范例

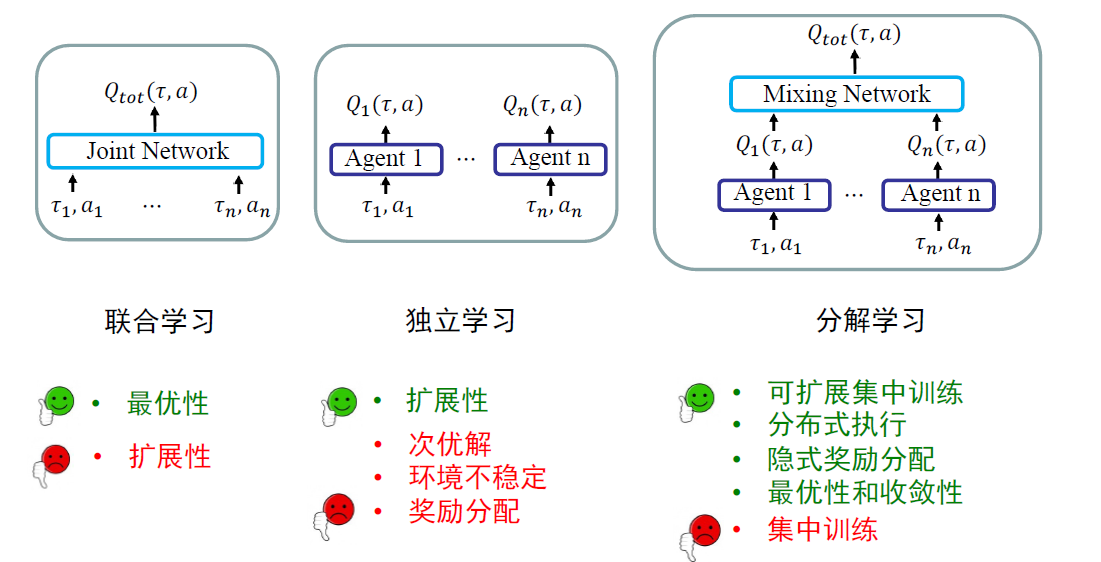
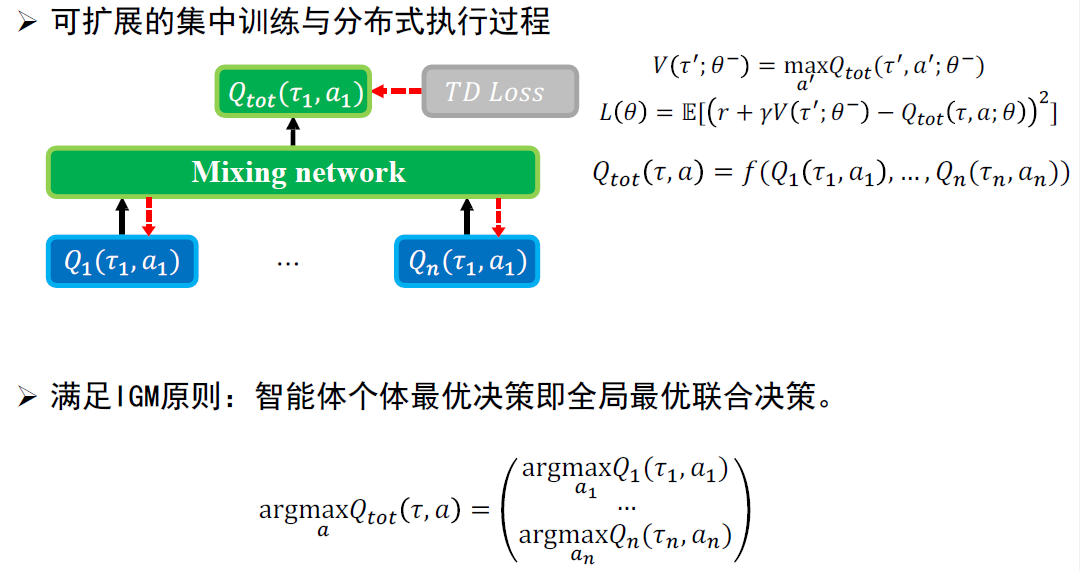
img image-20240709102207974

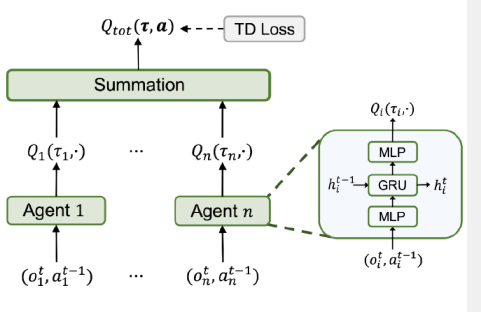
  1. 线性值分解：即\(Q_{tot}(\tau,a)=\sum_iQ_i(\tau_i,a_i)\), VDN算法
    • 满足IGM
    • 混合网络无参数，Q直接相加
    • 对每个智能体没有直接的独特的奖励分配
    • 在神经网络梯度回传时完成隐式奖励分配
    • 理论保证，参考Multi-Agent Fitted Q-Iteration框架
image-20240709102717861
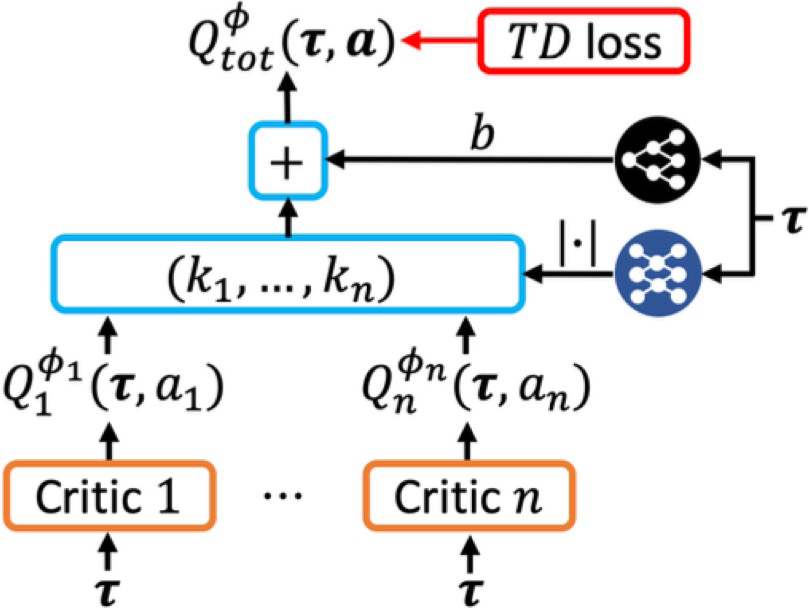
  1. DOP算法：引入线性可分解的critic网络，即\(Q_{tot}^\pi(\tau,.)=\sum_ik_i(\tau)Q_i(\tau,.)+b(\tau)\)，其中\(\tau\)为联合历史数据
    • 简单实用
    • 支持离线MARL，并能减小方差
    • 在策略单调提升的前提下收敛有理论保证
    • 适合离散和连续行为空间
image-20240709102914463

  1. 线性分解局限性：有限的表征能力，没有全局收敛保证

  2. QMIX：引入单调混合网络函数，即\(\dfrac{\partial Q_{tot}}{\partial Q_i}\geq0\)(baseline)

    • 引入超网络，使得混合网络的网络参数被限定为非负。即每个智能体至少对群体的贡献为正

  3. QPLEX：Q-Learning with IGM Factorization

img

其他MARL方法

动态共享学习目标

  • 多智能体强化学习需要更大的样本量，所以参数共享作为减少样本量的方法，对于多智能体强化学习非常重要。
  • 在智能体学习中，智能体倾向于学习到均质行为策略，而实际上，不同的智能体在环境交互中往往需要异质性策略
  • 因此动态目标学习可以使智能体根据其目标最大化个体差异

ROMA

  • 相似角色的智能体分享相似的学习目标和分享相似的行为策略。
    • 相似角色\(\leftrightarrow\)相似子任务\(\leftrightarrow\)相似行为策略
  • 角色可以作为短期博弈轨迹的编码并嵌入到输入。
  • 智能体以对应的角色作为条件进行策略学习。
  • 智能体在不同的场景下动态更换其角色

价值分解局限性

  • 不确定性
    • 价值分解可以导致合作失调；
    • 在分布式执行的过程中也会导致行为浪费；
  • 因此可以引入智能体之间的交流

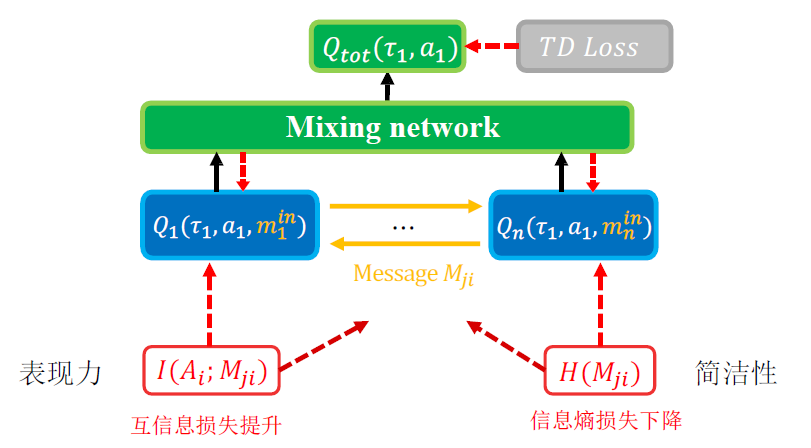
NDQ Nearly Decomposable Q-Value Learning

  • 允许智能体间交流，但是需要最小化交流信道
  • 智能体学习什么时候、向谁、交流什么内容
image-20240709110202109

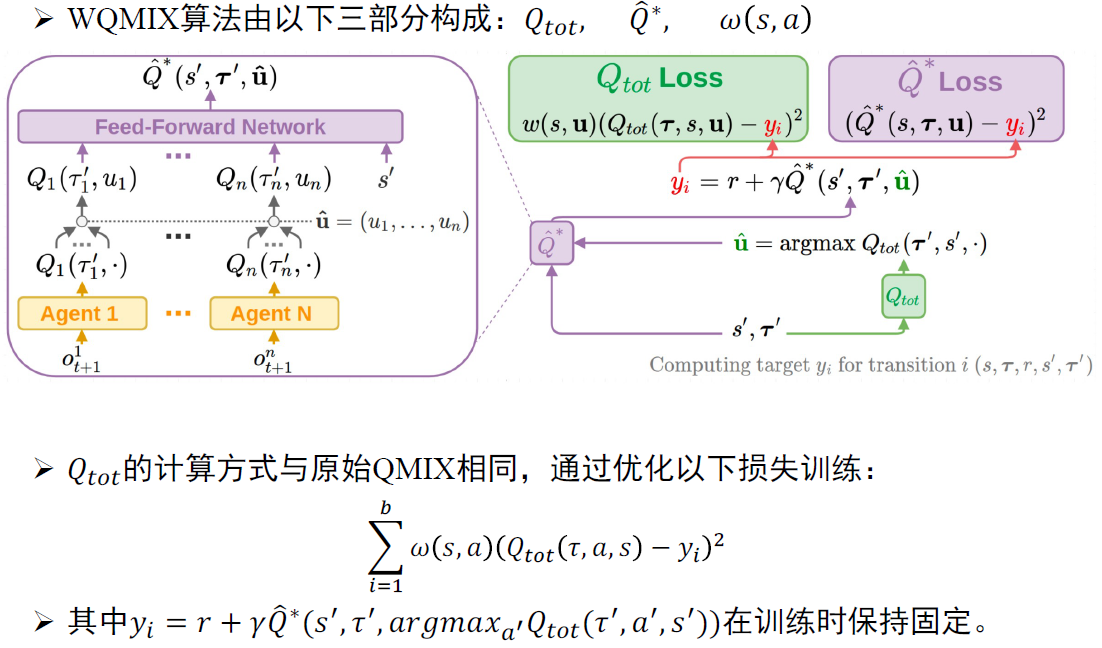
W-QMIX

  • QMIX问题
    • QMIX算法的单调性约束是充分不必要条件，即有些场景的值函数是QMIX无法精确拟合的。例如一个智能体的行为取决于另一个同队智能体时，QMIX是没有考虑的，同时IGM原则也被违反了。
    • \(\mathcal{J}^*_{Qmix}\)算子不是收缩映射，即QMIX算法找不到\(\mathcal{J}^*\)对应的不动点，而只能找到其最接近不动点的次优点，所以QMIX的优化结果可能不是唯一的。
    • QMIX可能会低估某些联合动作的价值。这是QMIX自身缺陷导致的，与计算性能、探索机制、及网络参数没有关系
  • 优化：增加权重函数 \(\pi_\omega Q=\arg\min\limits_{q\in Q^{mix}}\sum\limits_{a\in A}\omega(s,a)(Q(s,a)-y)^2\)
  • \(\omega(s,a)=1\)，即QMIX
imgimg

评论