Lec 6¶

6.1 策略学习高级技巧¶

From 《深度强化学习》第 9 章

TRPO¶

置信域策略优化 Trust Region Policy Optimization

优势：表现更稳定，对学习率不敏感；需要经验更少

置信域¶

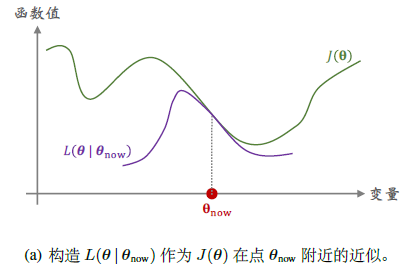
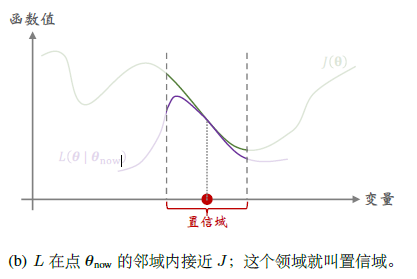
构造函数$L(\theta|\theta_{now})$，满足对$\forall\theta\in\mathcal{N}(\theta_{now})$，此函数很接近目标函数$J(\theta)$，其中$\mathcal{N}(\theta_{now})$为邻域。此时我们称此邻域为置信域，即在此范围我们可以信任$L(\theta|\theta_{now})$，用他代替目标函数

置信域方法：
- 第一步：做近似，给定$\theta_{now}$，构造函数$L$，满足如上定义。比如蒙特卡洛、二阶泰勒
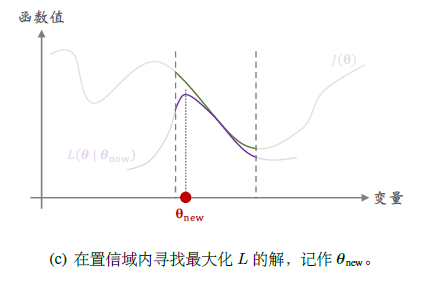
- 第二步：最大化，在置信域内寻找使得$L$最大的$\theta$，即$\theta_{new}=\arg\max\limits_{\theta\in\mathcal{N}(\theta_{now})}L(\theta|\theta_{now})$，需要解一个带约束的最大化问题，利用梯度投影算法、拉格朗日法等

Example

策略学习¶

状态价值的等价形式

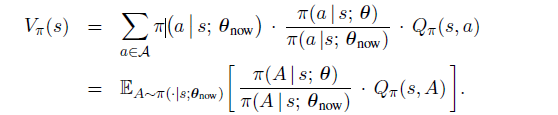
目标函数的等价形式

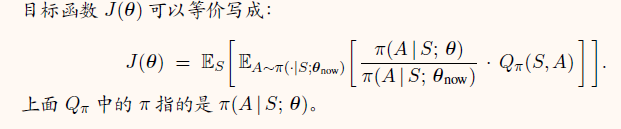
TRPO 训练流程¶

近似：
- 当前策略网络参数$\theta_{now}$，用策略网络$\pi(a|s;\theta_{now})$控制智能体与环境交互，记录轨迹：
$$ s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_n, a_n, r_n $$
- 对于所有$t=1,2,\cdots,n$，计算折扣回报$u_t=\sum_{k=t}^n\gamma^{k-t}\cdot r_k$
- 得出近似函数
$$ \tilde{L}(\theta|\theta_{now})=\dfrac{1}{n}\sum_{t=1}^n\dfrac{\pi(a_t|s_t;\theta)}{\pi(a_t|s_t;\theta_{now})}\cdot u_t $$
最大化：约束条件可以是二范数距离、KL 散度等
有两个需要调的超参，一是置信域半径$\Delta$，另一个是求解最大化问题的学习率

熵正则¶

我们希望策略网络输出的概率分布的熵不要太小

\[ H(s;\theta)\triangleq Entropy[\pi(\cdot|s;\theta)]=-\sum_{a\in\mathcal{A}}\pi(a|s;\theta)\cdot\ln\pi(a|s;\theta) \]

只依赖于状态 s 与策略网络参数$\theta$

我们可以得到需要求解的最大化函数，其中$\lambda$为超参

\[ \max_\theta J(\theta)+\lambda\cdot\mathbb{E}_S[H(S;\theta)] \]

这里使用策略梯度求解

\[ \nabla_\theta[J(\theta)+\lambda\cdot\mathbb{E}_S[H(S;\theta)]]=\mathbb{E}_S[\mathbb{E}_{A\sim\pi(\cdot|s;\theta)}[\tilde{g}(S,A;\theta)]] \]

6.2 连续控制¶

From 《深度强化学习》第 10 章

确定策略梯度¶

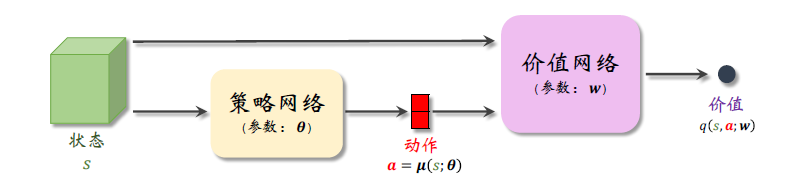
确定策略梯度(Deterministic Policy Gradient, DPG)，策略网络输出为 d 维的向量 a。对于确定的状态 s，策略网络$\mu$输出动作 a 是确定的，而非随机抽样。价值网络是对动作价值函数的近似，仅用来在训练的时候评价策略网络

算法推导¶

用行为策略收集经验：这里行为策略可以不同于目标策略，行为策略可以是任意的，可以使用过时的策略网络参数，而且可以往动作中加入噪声$\epsilon\in\mathbb{R}^d$，如$a=\mu(s;\theta_{old})+\epsilon$。通过异策略的方式，把收集经验和训练神经网络分隔开，把收集到的经验存入 replay buffer。我们把智能体的轨迹整理成$(s_t,a_t,r_t,s_{t+1})$，训练策略网络时只用到$s_t$，训练价值网络都要用到
训练策略网络：改进参数$\theta$，使得价值网络打分$\hat{q}$更大
目标函数: $J(\theta)=\mathbb{E}_S[q(S,\mu(S;\theta);w)]$
梯度上升: $g_j\triangleq \nabla_{\theta }q(s_j,\mu(s_j;\theta);w)$，是$\nabla_\theta J(\theta)$的无偏估计
利用链式法则: 其中$\hat{a}_j=\mu(s_j;\theta)$

$$ \nabla_{\theta }q(s_j,\mu(s_j;\theta);w)=\nabla_\theta\mu(s_j;\theta)\cdot\nabla_aq(s_j,\hat{a}_j;w) $$

因此我们如下更新$\theta$

$$ \theta\leftarrow\theta+\beta\cdot\nabla_\theta\mu(s_j;\theta)\cdot\nabla_aq(s_j,\hat{a}_j;w) $$

训练价值网络：让价值网络 q 的预测越来越接近真实价值函数，利用实际观测的奖励$r$来校正
首先让价值网络预测$\hat{q}_j,\hat{q}_{j+1}$,TD 目标$\hat{y}_j=r_j+\gamma\cdot\hat{q}_{j+1}$，定义损失函数，计算梯度，梯度下降更新
训练流程：每次从经验回放数组中抽取一个四元组，进行策略网络预测、价值网络预测、计算 TD 目标和 TD 误差、更新价值网络、更新策略网络

高估问题¶

TD 目标是对真实动作价值的高估
自举导致高估的传播

双延时确定策略梯度(TD3)¶

只改进 DPG 的算法而不改变结构。使用截断双 Q 和两个改进

解决高估问题¶

使用目标网络计算 TD 目标$\hat{y}_j$，有所缓解但高估仍然很严重
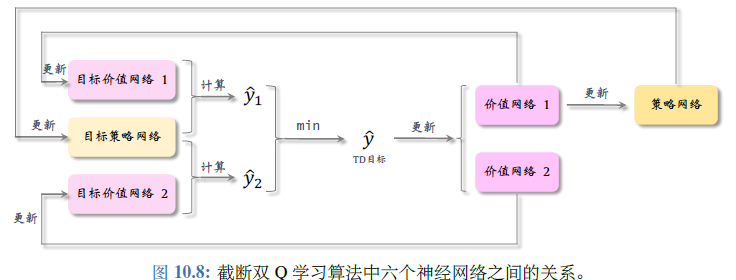
更好的方案：截断双 Q 学习(clipped double Q-learning)：使用两个价值网络和一个策略网络，三个神经网络各对应一个目标网络，用目标策略网络计算动作，两个目标价值网络分别计算$\hat{y}_j$，用较小的作为 TD 目标
进一步改进：
- 往动作中加噪声，即在用目标策略网络计算动作时，改成$\overline{\hat{a}_{j+1}}=\mu(s_{j+1};\theta^-)+\xi$，其中$\xi$为随机向量，每个元素独立随机从截断正态分布中抽取。这里记截断正态分布为$\mathcal{CN}(0,\sigma^2,-c,c)$，变量落在$[-c,c]$之外的概率为 0，这样可以防止噪声过大
- 减小更新策略目标和策略网络的频率：每隔 k 轮更新一次策略网络和三个目标网络。k 为超参

训练流程¶

每次从数组中随机抽取一个四元组，让目标策略网络预测、两个目标价值网络预测、计算 TD 目标、让两个价值网络做预测、计算 TD 误差、更新价值网络、每隔 k 轮更新策略网络和三个目标网络

随机高斯策略¶

策略梯度训练流程¶

搭建均值网络$\mu(s;\theta)$，方差对数网络$\rho(s;\theta)$，辅助网络$f(s,a;\theta)$
让智能体与环境交互，计算每一步的状态、动作、奖励，并对参数$\theta$更新
观测当前状态 s，计算均值、方差对数、方差;此处指数函数应用到向量的每一个元素

\[ \hat{\mu}=\mu(s;\theta), \hat{\rho}=\rho(s;\theta), \hat{\sigma}^2=\exp(\hat{\rho}) \]
设$\hat{\mu}_i$和$\hat{\sigma}_i$分别是第 i 个元素，从正态分布中采样$a_i\sim\mathcal{N}(\hat{\mu}_i,\hat{\sigma}_i^2)$，得到动作$\mathcal{a}=[a_1,a_2,\cdots,a_d]$
近似计算动作价值 $\hat{q}\approx Q_\pi(s,a)$
用反向传播计算出辅助网络关于参数$\theta$的梯度 $\nabla_\theta f(s,a;\theta)$
用策略梯度上升更新参数 $\theta\leftarrow\theta+\beta\cdot\hat{q}\cdot\nabla_\theta f(s,a;\theta)$

REINFORCE¶

用实际观测的折扣回报$u_t=\sum_{k=t}^n\gamma^{k-t}r_k$代替动作价值，可以将策略梯度近似成$g\approx u_t\nabla_\theta f(s,a;\theta)$，重复一以下步骤直到收敛：

效果不如使用基线的 REINFORCE

用 AC 学习参数¶

略