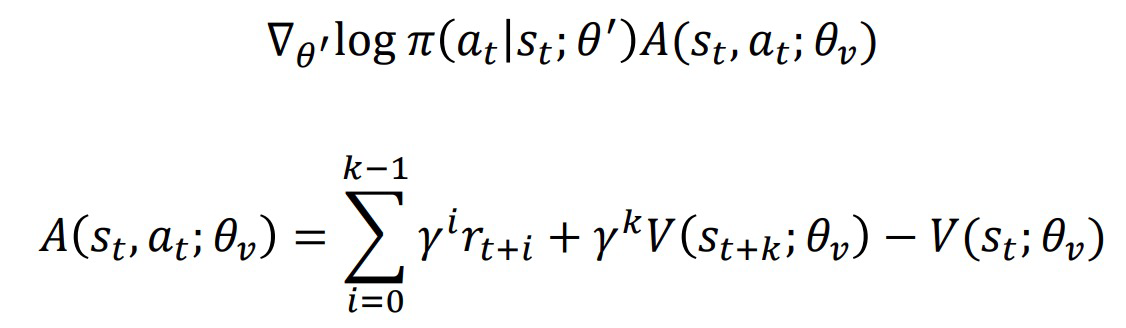5 Policy Gradient

Recall

\(\pi_\theta(a|s)=P(a|s,\theta)\)

• 策略参数化
  • 优点
    • 收敛性质好
    • 在高维度或连续的动作空间中更有效
    • 能够学习出随机策略
  • 缺点
    • 会陷入局部最优
    • 评估一个策略通常不够高效并具有较大的方差

策略梯度

基于策略的强化学习方法

• 不需要价值函数
• 直接学习策略
• 高维或连续动作空间场景中更加高效
• 适用任何动作类型的场景

• 容易收敛到次优解

• 直接搜索最优策略\(\pi^*\)

参数化策略

• 参数化策略\(\pi_\theta\)​，并利用无梯度或基于梯度的优化方法对参数进行更新
  • 无梯度优化可以有效覆盖低维参数空间
  • 但基于梯度的训练仍然是首选，因为其具有更高的采样效率

• 参数化策略和表格型策略对比

  • 采取动作的概率的计算方式不同：前者通过给定的函数结构和参数计算\(\pi_\theta(a|s)\)，后者直接查对应s和a表
  • 策略更新方式不同：前者更新\(\theta\)，后者直接修改表格对应条目
  • 最优策略定义不同：前者最大化一个给定的标量指标\(π^\#(s) = \arg\max_πJ(π(s))，π∈Π\) ，后者最大化每个状态对应值函数

• 将参数化策略\(π_θ\)所能表示的所有策略组成的集合记为策略容许集\(Π={π_θ:θ∈Θ}\)，\(Θ\)为参数\(θ\)的取值范围

  • 若\(π^*∈Π\)，则有\(J(π^\#) = J(π^*)\)
  • 若\(π^*∉Π\)，则策略\(π^*\)比\(π^\#\)更优

基本思想

• 利用目标函数定义策略优劣性:\(J(\theta)=J(π_\theta)\)

• 对目标函数进行优化，以寻找最优策略

• 优化方向：可微分用基于梯度，否则无梯度算法，如有限差分、交叉熵、GA

目标函数

• 状态分布

  • 策略无关：一种简单的做法是取\(d(s)\)为均匀分布，另一种做法是把权重集中分配给一部分状态集合，例如一些任务只从\(s_0\)开始，则\(d(s_0)=1,d(s\neq s_0)=0\)
  • 策略相关：通常采用稳态状态分布，若对状态转移\(s\rightarrow a\rightarrow s'\)，满足
  \[ d(s')=\sum_{s\in\mathcal{S}}\sum_{a\in\mathcal{A}}p(s'|s,a)\cdot\pi_\theta(a|s)\cdot d(s) \]

计算策略梯度

• 如梯度下降、牛顿迭代
• 以最大化平均轨迹回报目标函数为例,\(\tau\)为\(\pi_\theta\)采样得到轨迹\(\{s_1,a_1,r_1,s_2,a_2,r_2,\cdots,s_T\}\)

\[ \max_\theta J(\theta)=\max_\theta \mathbb{E}_{\tau\sim p_\theta(\tau)}[\sum_t r(s_t,a_t)] \]

• 记\(G(\tau)=\sum_t r(s_t,a_t)\)，平均轨迹回报目标的策略梯度为

• 不同目标函数可以得到上述策略梯度，从而对策略进行优化\(\theta_{t+1}\leftarrow\theta_t+\nabla_\theta J(\theta)\)

策略梯度算法

Reinforce

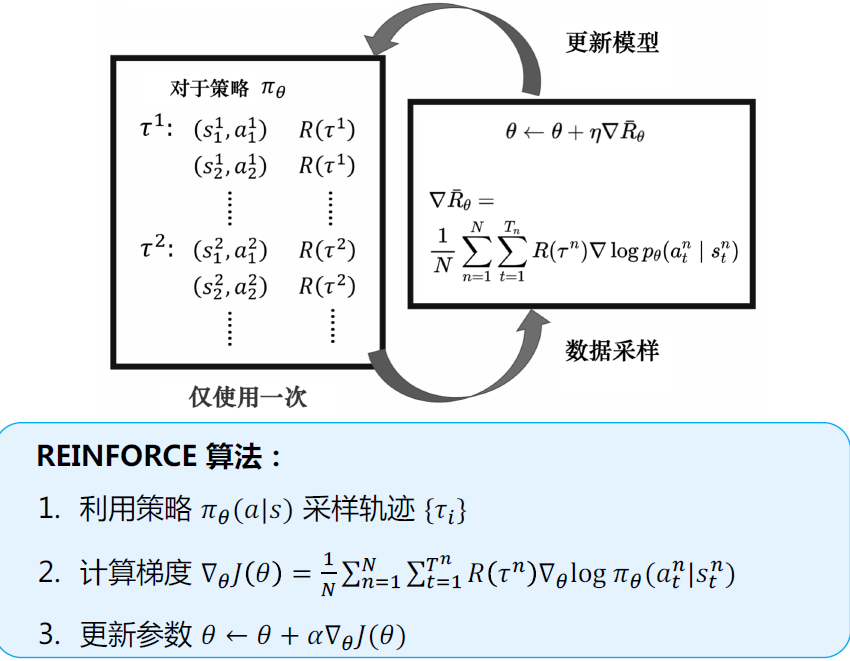
1. 添加baseline

   • 训练可能存在偏差：考虑只有正奖励，在理想情况下进行优化，最终能够使得奖励值高的动作分配较高的采样概率，而奖励值低的动作分配较低的采样概率，但在实际场景中我们可能并不能采样到所有的动作，如只能采样到b和c ，这就会使得我们的优化有所偏差：
   
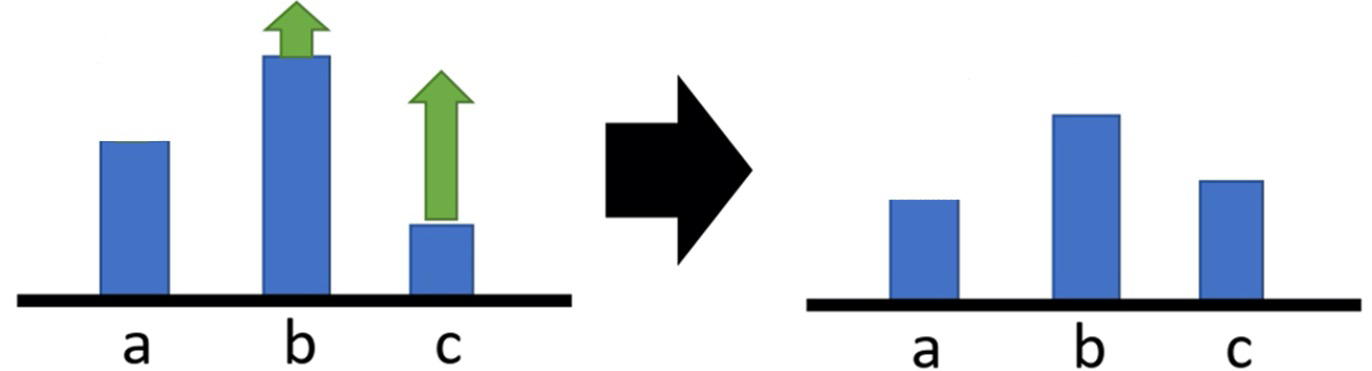
   • 我们可以将奖励函数减去一个基线𝑏，使得\(𝑅(𝜏) − 𝑏\) 有正有负
     • 如果\(𝑅(𝜏) > 𝑏\)，就让采取对应动作的概率提升
     • 如果\(𝑅(𝜏)< 𝑏\)，就让采取对应动作的概率降低
   • 一般取\(b=\dfrac{1}{N}\sum\limits_{i=1}^NR(\tau)\)，训练时记录\(R(\tau)\)的值并维护平均值
   • 减去一个基线并不会影响原梯度的期望值
   

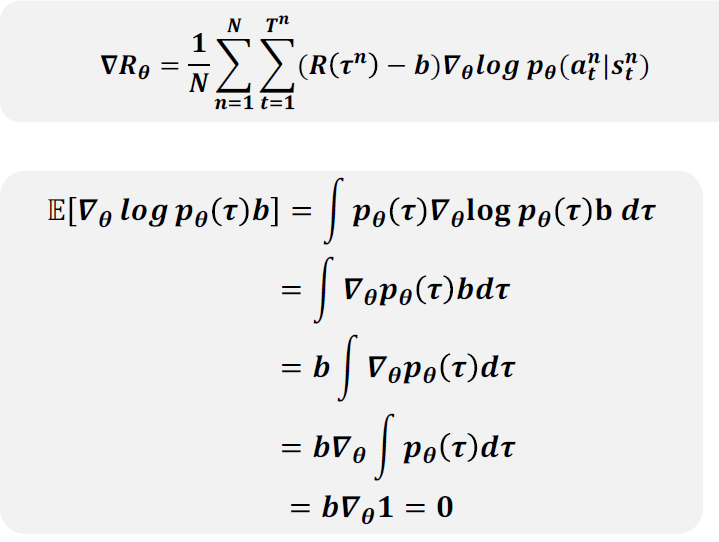
2. 实现策略梯度：利用自动求导工具实现

   • 将策略梯度的目标函数视为极大似然法的目标函数一个利用累积奖励进行加权的版本

3. 策略梯度存在问题

   • 为同策略算法，样本利用率较低
   • 较大的策略更新或不适宜的更新步长会导致训练的不稳定
     • 不适宜更新步长 \(\rightarrow\) 坏策略 \(\rightarrow\) 低质量的数据
     • 可能难以从糟糕策略中恢复，导致性能崩溃
4. 离策略梯度：根据重要性采样利用异策略样本

5. 自然策略梯度： \(d^*=\arg\max\limits_dJ(\theta+d), s.t. KL(\pi_\theta||\pi_{\theta+d})=c\)

   • KL散度用于衡量两个分布的接近程度

     \[KL(\pi_\theta||\pi_{\theta'})=\mathbb{E}_{\pi_\theta}[\log\pi_\theta]-\mathbb{E}_{\pi_{\theta'}}[\log\pi_{\theta'}]\]

   • 将更新前后策略的KL散度限定为一个常数c，确保策略分布以一个常量速度更新，而不受策略的参数化形式影响

   • 将KL散度进行二阶泰勒展开，\(KL(\pi_\theta||\pi_{\theta+d})\approx \dfrac{1}{2}d^TFd\)，其中F为Fisher Information Matrix，即

   $$ \mathbb{E}{\pi\theta}[\nabla\log\pi_\theta\nabla\log\pi_\theta^T] $$

   
   • 从而得到\(\theta_{t+1}=\theta_t+\alpha F^{-1}\nabla_\theta J (\theta)\)，其更新效果与模型的参数化无关

Actor-Critic算法

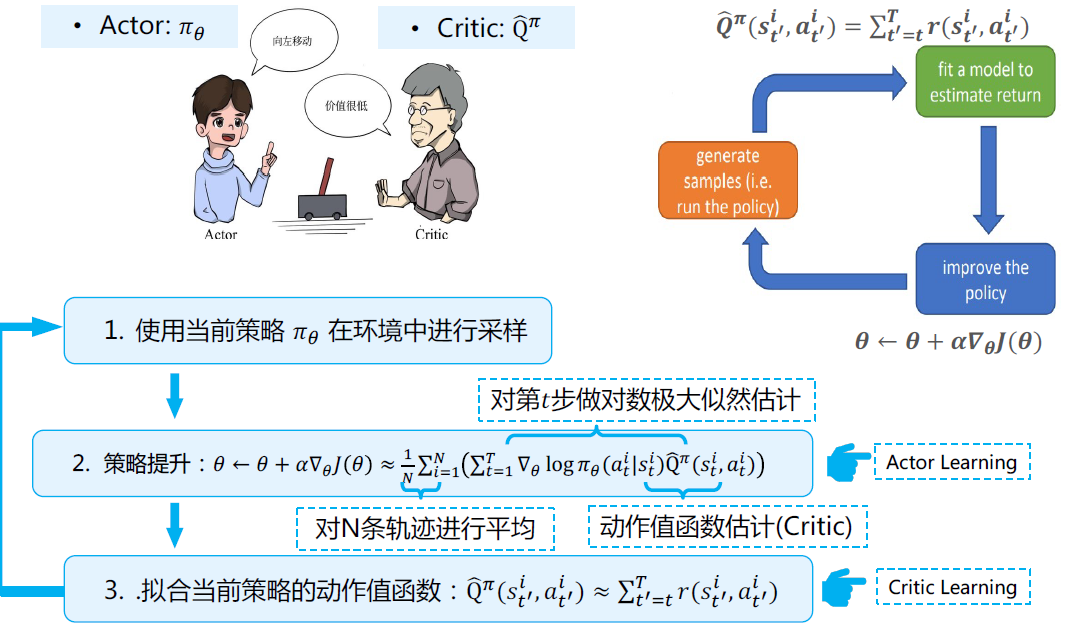
• 策略梯度并利用优势函数\(\hat{A}^\pi(s_t^i,a_t^i)=\hat{Q}^\pi(s_t^i,a_t^i)-\hat{V}^\pi(s_t^i)\) $$ \nabla_\theta J(\theta)\approx\dfrac{1}{N}\sum_{i=1}^N(\sum_{t=1}^T\nabla_\theta\log\pi_\theta(a_t^i|s_t^i)\hat{A}^\pi(s_t^i,a_t^i)) $$

• 思想：通过减去一个基线值来标准化评论家的打分

  • 降低较差工作概率，提高较优动作概率
  • 进一步降低方差

\[\nabla_\theta J(\theta)\approx\dfrac{1}{N}\sum_{i=1}^N(\sum_{t=1}^T\nabla_\theta\log\pi_\theta(a_t^i|s_t^i)\hat{A}^\pi(s_t^i,a_t^i)) \]

\[ \approx\dfrac{1}{N}\sum_{i=1}^N(\sum_{t=1}^T\nabla_\theta\log\pi_\theta(a_t^i|s_t^i)[\hat{Q}^\pi(s_t^i,a_t^i)-\hat{V}^\pi(s_t^i)]) \]

\[ \approx\dfrac{1}{N}\sum_{i=1}^N(\sum_{t=1}^T\nabla_\theta\log\pi_\theta(a_t^i|s_t^i)[R(s_t^i,a_t^i)+\gamma\hat{V}^\pi(s_{t+1}^i)-\hat{V}^\pi(s_t^i)]) \]

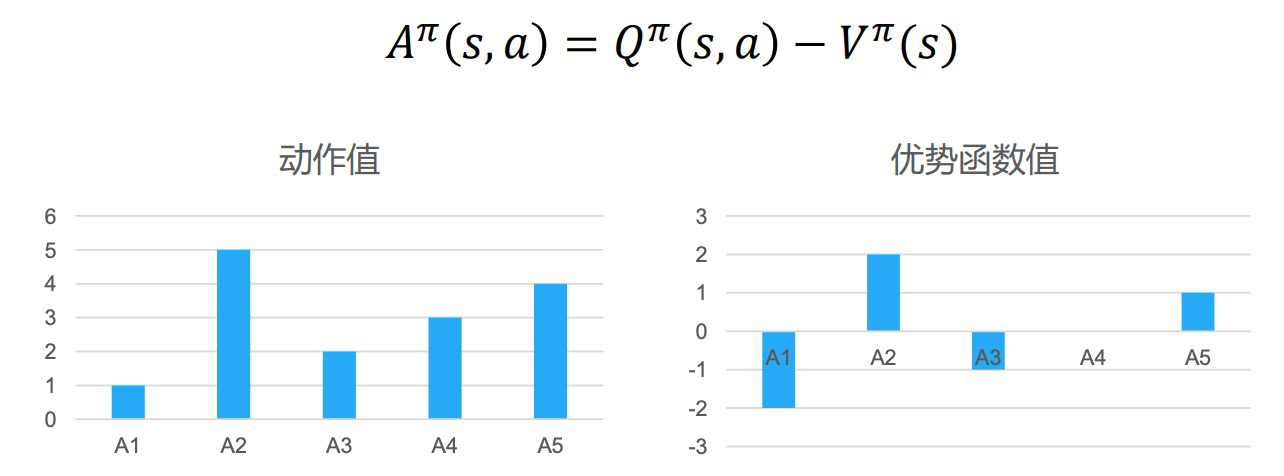
• 只需要用一个神经网络拟合\(\hat{V}^\pi\)

• 深度A2C算法

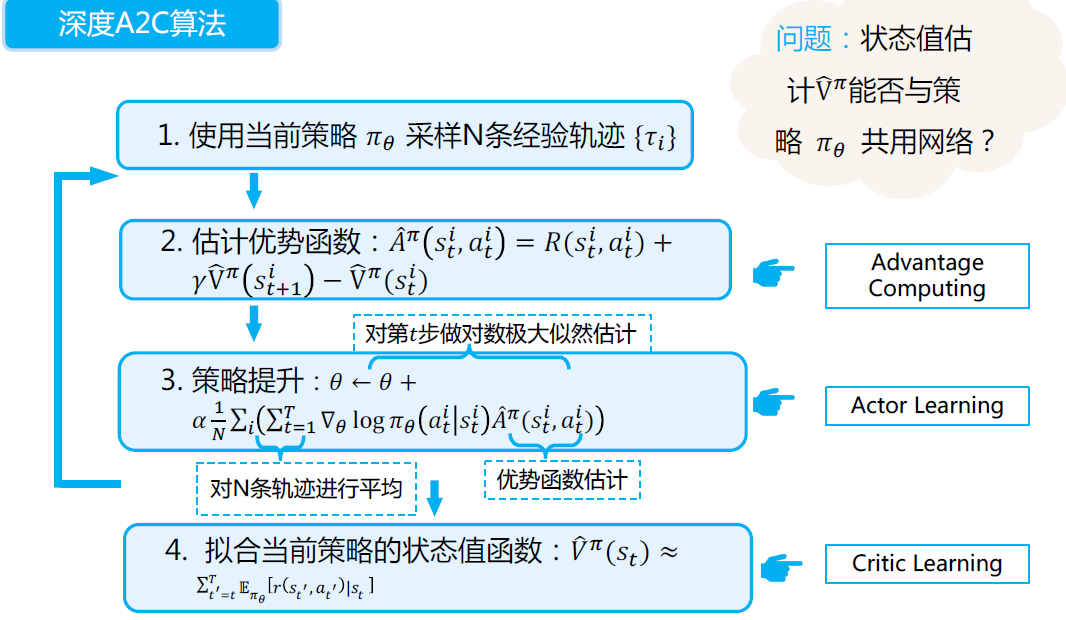
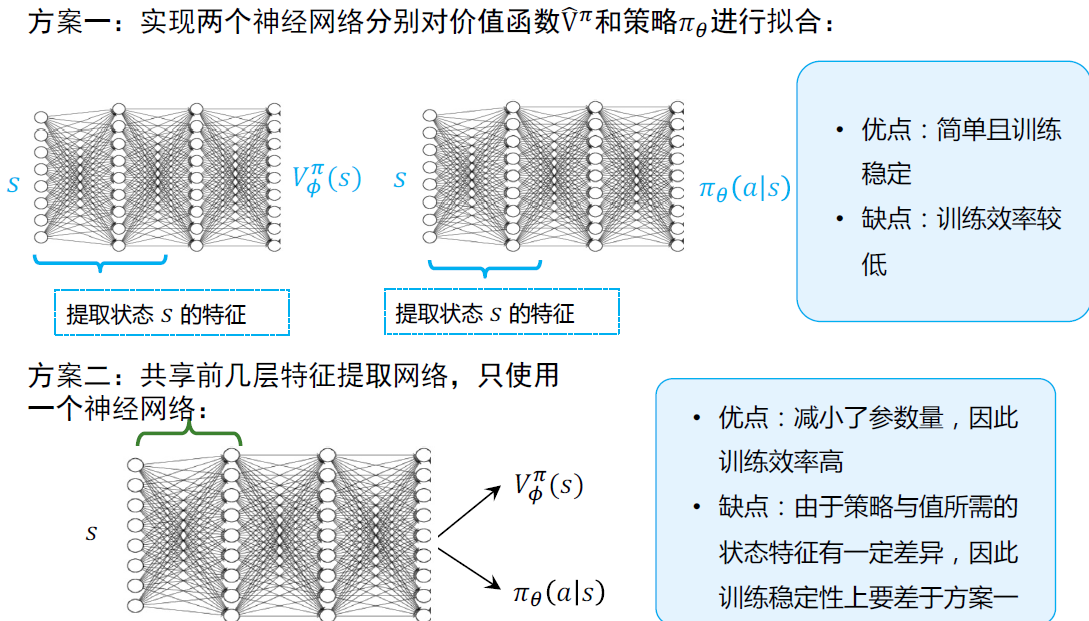
• 批量更新：获得一个batch的数据后再进行更新，同样和上一节类似有同步和异步

A3C算法

Asynchronous A2C，涉及执行一组异步并行的环境，和A2C一样使用优势函数。充分利用GPU资源

评论