4 Deep Q Network¶

探索与利用¶

$\epsilon$-greedy¶

$\epsilon$可以设定为超参，也可以随训练进行衰减

UCB¶

$Q(a)\leq\hat{Q}_t(a)+\hat{U}_t(a)$,其中上界函数$\hat{U}_t(a)$与$N_t(a)$相关，大行为访问次数导致较小的置信上界
Hoeffding不等式: $$ \mathbb{P}[Q(a)>\hat{Q}_t(a)+U_t(a)]\leq e^{-2tU_t(a)^2} $$
- 我们令$p=e^{-2tU_t(a)^2}$,则$U_t(a)=\sqrt{\dfrac{-\log p}{2N_t(a)}}$
- 一种启发方法是及时降低p的阈值，设定$p=t^{-4}$,则$U_t(a)=\sqrt{\dfrac{2\log t}{N_t(a)}}$
- 因此就有 $$ a_t^{UCB1}=\arg\max_{a\in A}(Q(a)+\sqrt{\dfrac{2\log t}{N_t(a)}}) $$
- 更一般地，$U_t(a)=\sqrt{\dfrac{c\log t}{N_t(a)}}$

蒙特卡洛树搜索¶

核心思路：不需要手动设计一个关于状态的启发函数，而是从该状态开始随机模拟一局博弈获得胜负信息。
增加UCB计算可以给状态更好的预估价值。
MCTS迭代：选择、扩展、模拟、回传
- 选择过程：递归选择最大UCB值的子节点
- 扩展过程：为子节点扩充未访问的节点并加进蒙特卡洛树中
- 模拟过程：从新扩展的节点开始，采用固定的策略进行博弈模拟（rollout），直到博弈结束。
- rollout过程采用任何策略皆可
回传过程：将模拟的结果递归回传到路径经过的所有节点直到根节点。
- 一般更新节点价值和节点访问次数
- 如果预存节点UCB值，则更新该路径上所有节点的子节点的UCB值
优势
- 在无专家知识的时候很有效；
- 节点大量模拟后可以逼近真实节点价值；
- MCTS过程可以并行化，例如可以在扩展的节点上进行多进程并行模拟；
劣势
- MCTS的计算结果有较大的方差；
- 模拟过程的策略对搜索效率有较大影响；

深度Q网络¶

将表格式的$Q(s,a)$的取值用神经网络代替，且该网络以状态+行为作为输入，以该状态行为价值作为输出，那么Q-learning算法就可以直接扩展为深度Q学习。

以学习目标 $r + \gamma \max\limits_{a' \in \mathcal{A}} Q(s', a') $ 来增量式更新$(s, a)$，即令 $Q(s, a)$贴近其 TD 目标。
- 状态价值网络： $Q_\omega(s, a)$
- 时序差分目标结果：$r + \gamma \max\limits_{a'} Q_\omega(s', a')$
给定一组状态转移数据： $\{(s_i, a_i, r_i, s'_i)\}$，深度 Q 网络的损失函数构造成为均方误差形式：

$$ \omega^* = \arg\min_\omega \frac{1}{2N} \sum_{i=1}^N \left[ Q_\omega(s_i, a_i) - \left( r_i + \gamma \max_{a'} Q_\omega(s'_i, a') \right) \right]^2 $$
Fitted Q值迭代算法：
1. 通过某些策略收集状态转移数据集 ${ (s_i, a_i, r_i, s_i') } $
2. 计算TD目标：$y_i \leftarrow r_i + \gamma\max\limits_{a_i'} Q_{\alpha}(s_i', a_i') $
3. 更新网络参数：$ \omega \leftarrow \arg\min\limits_{\omega} \frac{1}{2} \sum_i||Q_\omega(s_i, a_i) - y_i||^2 $
在线Q值迭代算法：
1. 环境中根据策略采取行为$a_i$，并从环境获取奖励$(s_i, a_i, r_i, s’_i)$
2. 计算TD目标：$y_i \leftarrow r_i + \gamma \max\limits_{a’_i} Q_{\omega}(s’, a’)$
3. 更新网络参数：$\omega \leftarrow \omega-\alpha \dfrac{dQ_\omega}{d\omega} (s_i, a_i)(Q_\omega(s_i, a_i) - y_i)$
存在问题：
- 神经网络训练需要独立同分布数据，但是状态转移数据强相关；
- 更新神经网络参数并不是梯度下降，$y_i$的计算也更新梯度；
- Q值的更新不稳定
  - 原因：对于同样的状态转移数据，短时间内同样的输入得到不同的TD目标作为监督信号
解决数据相关性：并行Q-learning，用其他进程的状态转移更新

经验回放缓存：不通过某些策略收集数据，而是从经验回放缓存中采样；经验回放缓存中数据来源于任何策略都可以

解决后两个问题：通过目标网络，TD目标阶段性保持不变且不参与梯度回传
经典深度Q学习
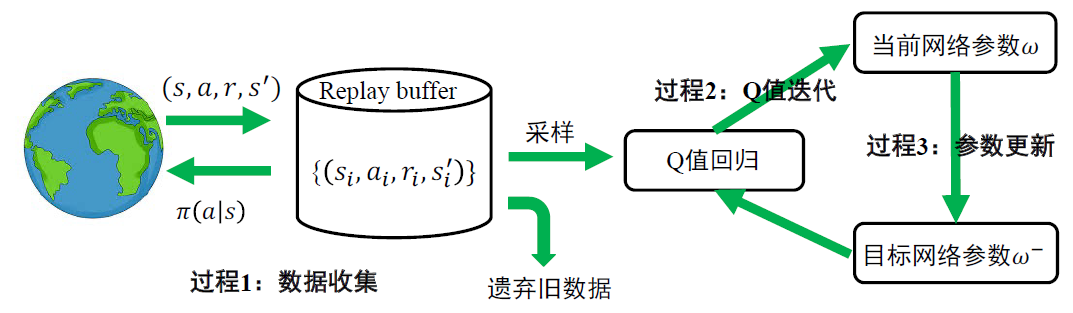
- 更新目标网络参数可以采用滑动平均的方法，即$\omega^-\leftarrow\tau\omega^-+(1-\tau)\omega,\tau=0.99$
- 这种方法在为新$\omega^-$赋值时可以保留旧有的$\omega$的影响

DQN改进算法¶

Q值过高估计
- 基于Boostrapping算法的价值估计的共有问题
- 原因：最大值的期望大于期望的最大值，算法总是选择价值最高的动作作为目标进行更新
Double DQN：选择动作和计算价值不使用同一个网络，使用两个网络分别进行目标值计算与动作选择，如果两个网络的误差不同，则可以在一定程度上解决问题

\[ Q_{\omega_1}\leftarrow r+\gamma Q_{\omega_2}(s',\arg\max_{a'}Q_{\omega_1}(s',a')) \]

Dueling DQN：将原来的Q网络拆分成两个部分：V网络和A网络
- V网络：以状态为输入、以实数为输出的表示状态价值的网络
- A网络：优势网络，它用于度量在某个状态𝑠下选取某个具体动作𝑎的合理性，它直接给出动作𝑎的性能与所有可能的动作的性能的均值的差值。如果该差值(优势)大于0，说明动作𝑎优于平均，是个合理的选择；如果差值(优势)小于0，说明动作𝑎次于平均，不是好的选择
- 一般来说：$Q(s,a)=V(s)+A(s,a)$
- 分辨当前的价值是由状态价值提供还是行为价值提供，进而有针对性的更新，增加样本利用率
优先经验回放池PER：一般来说，具有较大TD误差的样本应该给予更高的优先级
- 采样第$t$个样本的概率$p_t$正比于TD误差$\delta_t$,即$p_t\propto|\delta_t|+\epsilon$，其中$\epsilon$为小正数，防止采样概率为0
- 或反比于误差排位$p_t\propto\dfrac{1}{rank(t)}$
- 第二种更鲁棒
- 引入参数$\beta\in[0,1]$调整学习率 $\alpha_t\leftarrow\alpha(np_t)^{-\beta}$
  - 均匀采样时，$p_i=\dfrac{1}{n},(np_t)^{-\beta}=1$，学习率均为$\alpha$，回归普通的经验回放池
  - 基于优先采样时，具有高优先级的样本使用较低的学习率