1 Dynamic Programming

1. 有限步(N)期望累计奖励

   \[ J^{\Pi}_N(i)=E[\alpha^NG(i_N)+\sum\limits_{k=0}^{N-1}\alpha^kg(i_k,\mu_k(i_k),i_{k+1})|i_0=i] \]
   • 一阶段决策 最小化cost
   \[ J^*_1(i)=\min\limits_{u\in U(i)}\sum\limits_{j=1}^np_{ij}(u)(g(i,u,j)+\alpha G(j)) \]
   • k阶段决策
   \[ J^*_k(i)=\min\limits_{u\in U(i)}\sum\limits_{j=1}^np_{ij}(u)(g(i,u,j)+\alpha J^*_{k-1}(j)) \]

Example:最短路径案例

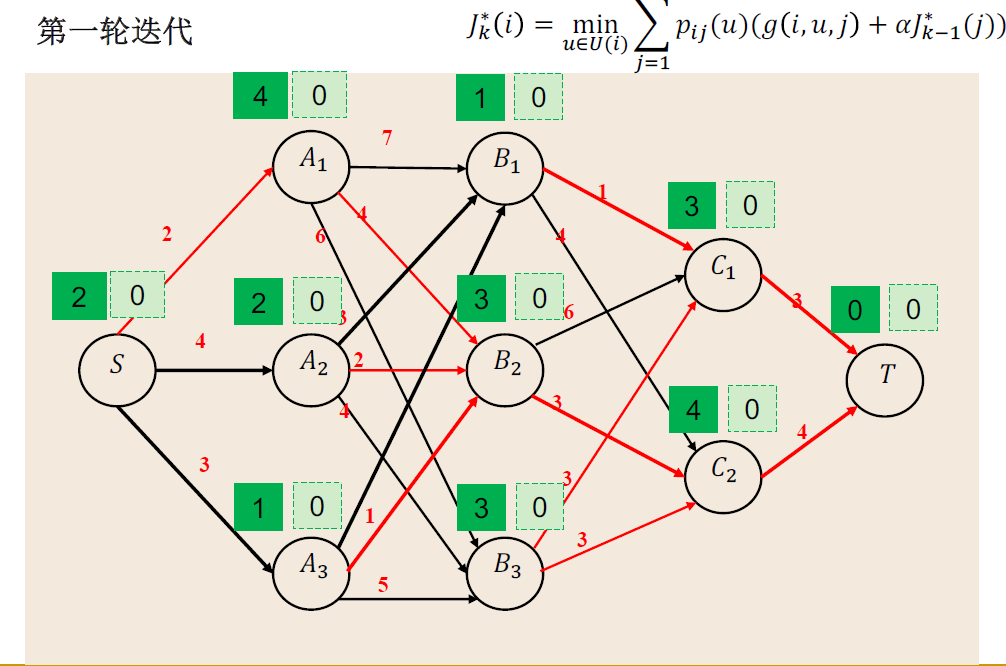
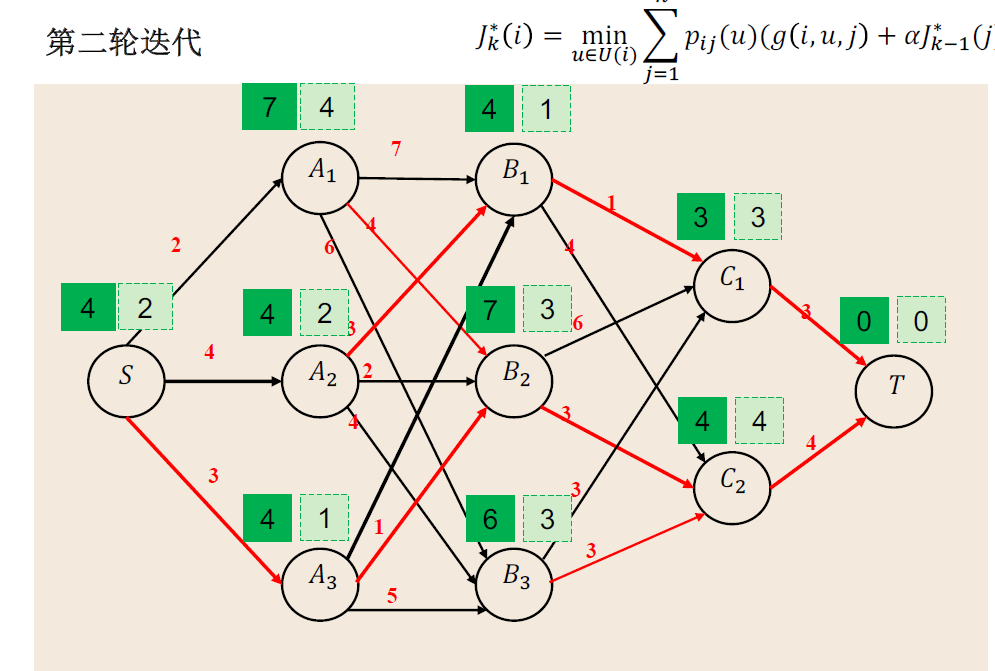
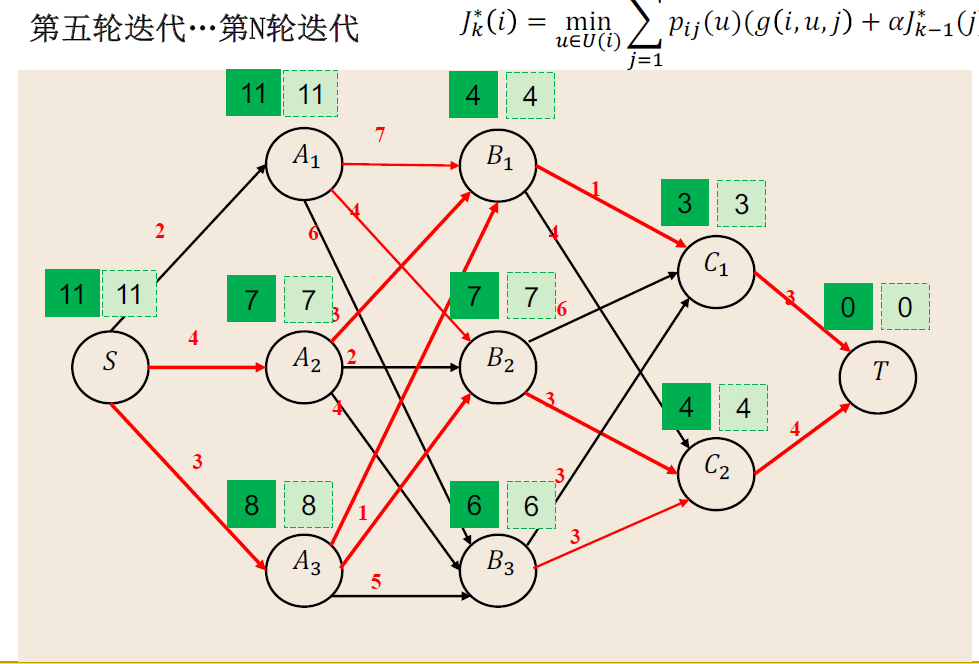
一般理论

1. 给定策略，不论初始状态，n轮决策后进入终止状态概率为正，则该策略为合理策略

\[ \rho_\mu=\max\limits_{i=1,\cdots,n}P(i_n\neq0|i_0=i,\mu)<1 \]

2. 动态规划速记符号:

一般来说\(T\)和\(T_\mu\)具备如下特性

3. 在前面的最短路径问题，假设至少有一个合理策略以及每一个不合理策略都至少有一个状态成本无限大，则
   • 最优未来成本(奖励)\(J^*\)变量是有限元，且是\(J=TJ\)的唯一解
   • 给定每一个向量\(J,\lim\limits_{k\rightarrow\infty}T^kJ=J^*\)
   • 对策略\(\mu\)和\(T_\mu\)上述同样适用
4. 证明DP的正确性，by收缩映射

MDP建模

1. 马尔科夫过程\(M=<S,A,P,R,Y>\)包括状态集合、行为集合、状态转移函数、奖励函数、未来奖励衰减系数
   • 在一个未知环境中，转移概率P和奖励R由环境给出，无法获取全部信息

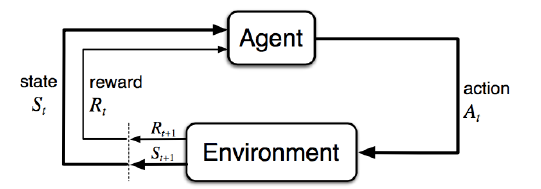
1. POMDP：部分可观测，带有隐藏状态的MDP，\(M=<S,A,O,P,R,Z,\gamma>\)

3. Bellman方程

AI导的残存记忆卷土重来

Bellman期望方程

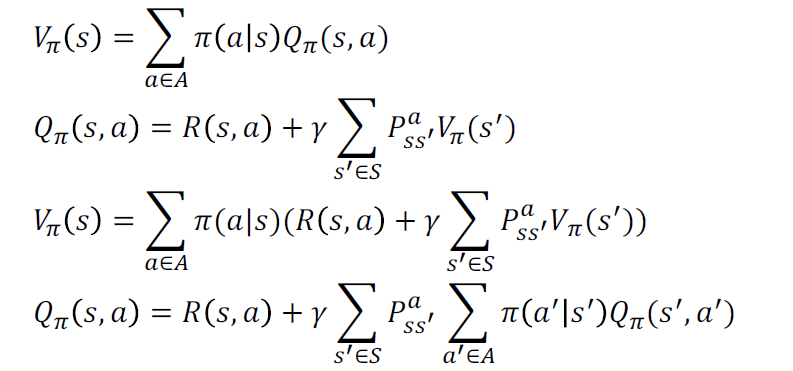
Bellman最优方程

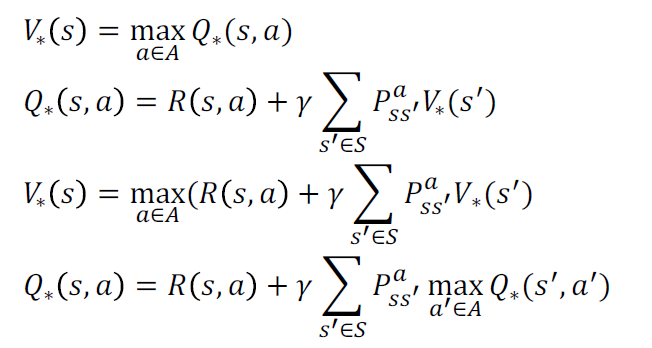
策略评估与优化

• 对于给定的策略\(\pi\)，策略评估用于计算状态价值函数

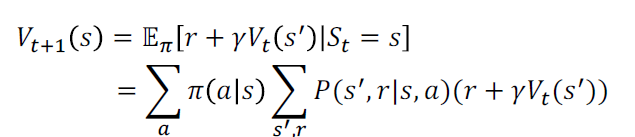
• 基于价值函数，策略优化通过更贪婪的行为生成更好的策略\(\pi'\geq\pi\)，且不会更坏

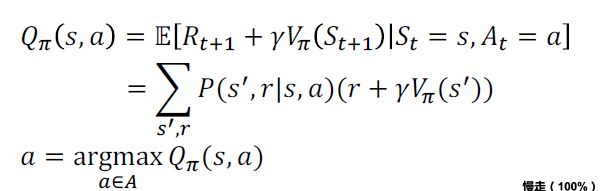
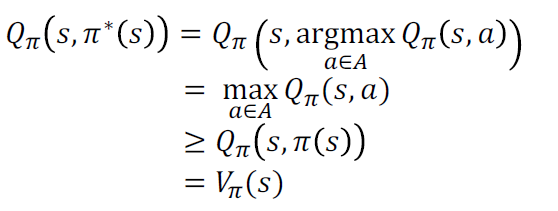
• 一般策略迭代算法将策略评估和策略优化相结合，每次策略执行后评估、优化再执行

• 在GPI中，价值函数可以通过重复迭代来不断接近当前策略的实际值;策略也在此过程中不断接近最优策略:且总是可以收敛到最优策略

评论