Lec.07: Structure from Motion

Problems to be noticed

• 相机怎么把三维点映射到图像平面 by camera model
• 怎么计算相机在世界坐标系下的位置和旋转 camera calibration and pose estimation
• 从图片重建3D结构 structure from motion

Camera model

1. Image Formation:世界坐标系->相机坐标系->像平面->像素坐标

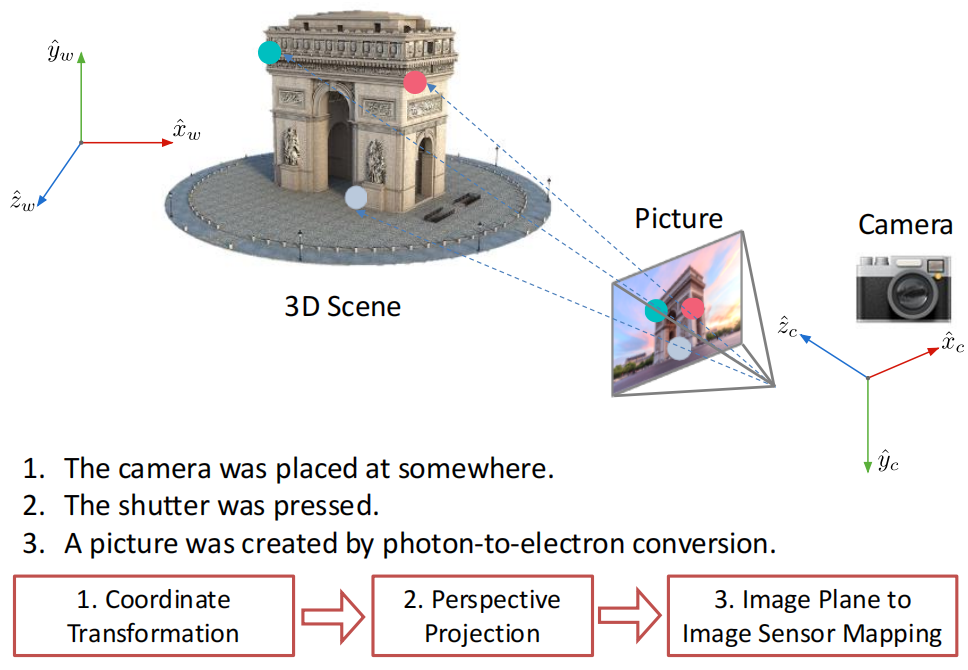
2. 相机坐标系对齐到世界坐标系 extrinsic parameters包括相机坐标和旋转角度\((R,c_w)\),R是正交单位阵

   
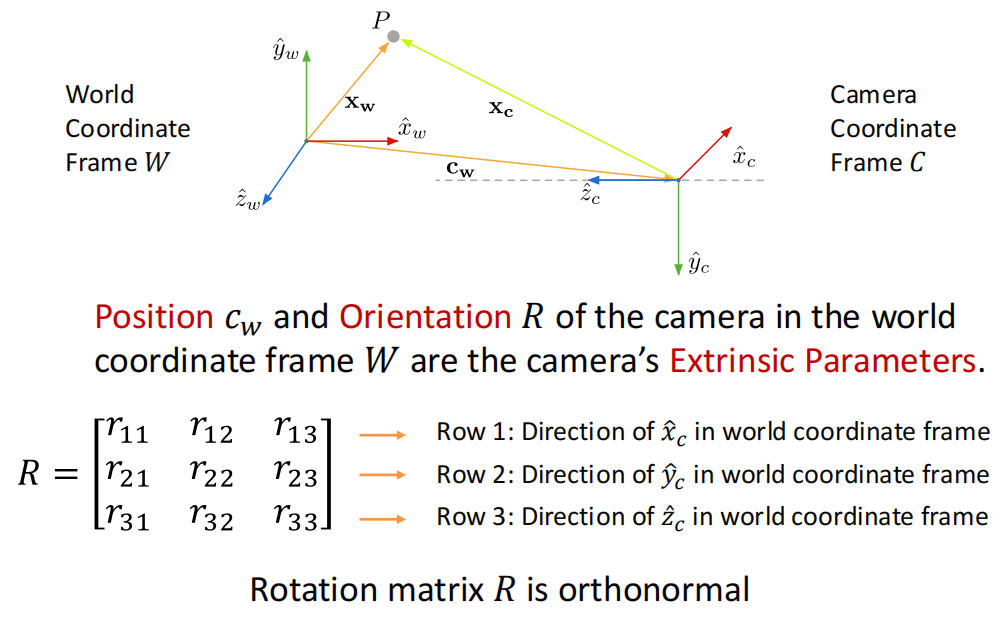
   • world-to-camera transformation
   
   • 齐次坐标系下
   

3. camera coordinate投影到image plane

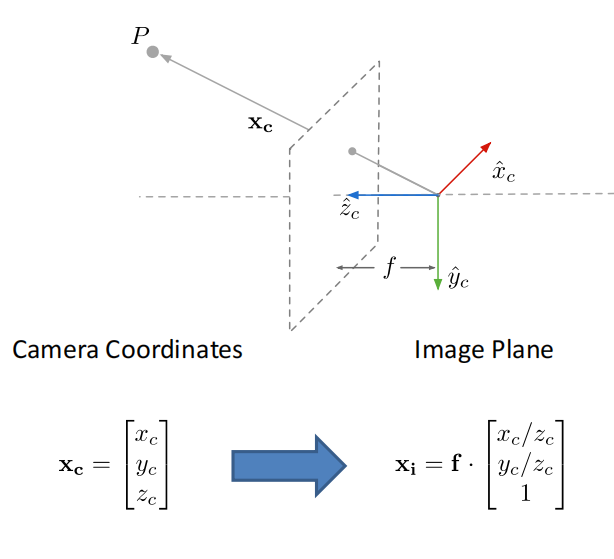
4. image plane to image sensor mapping by intrinsic matrix

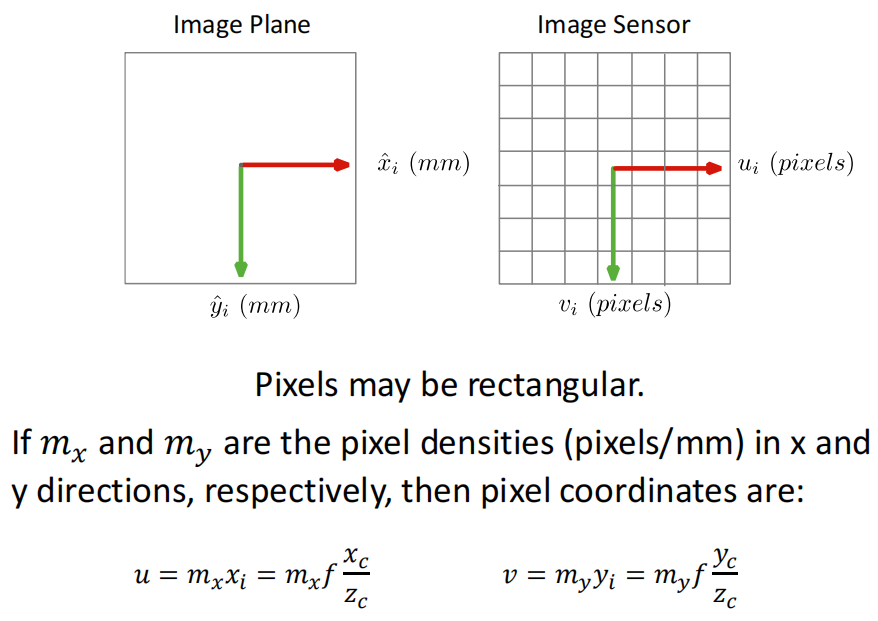
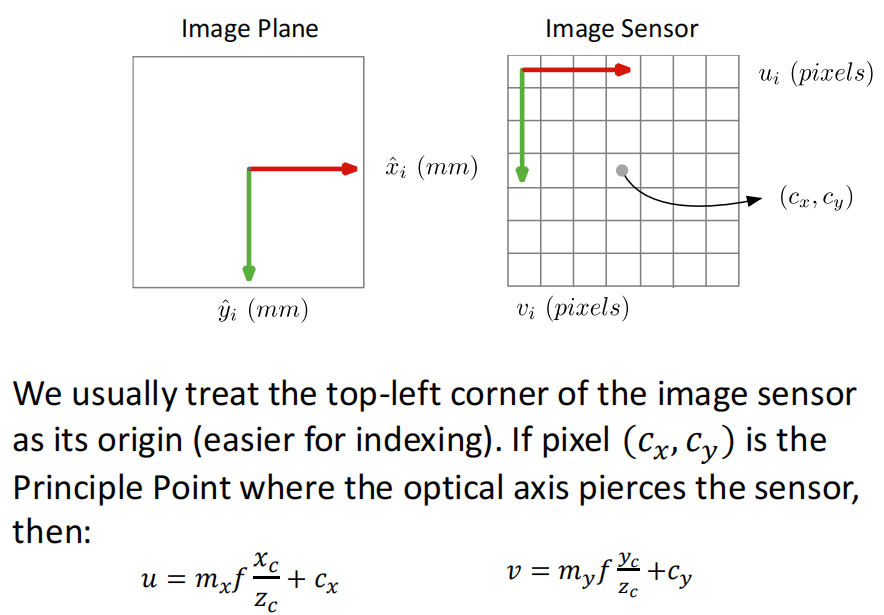
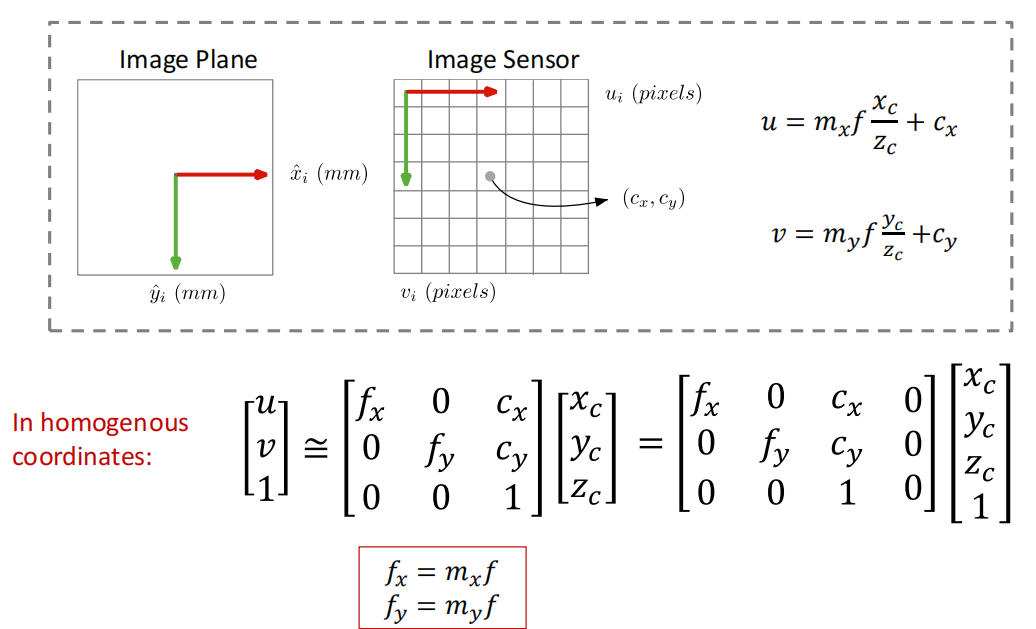
5. 总的projection matrix \(P\)

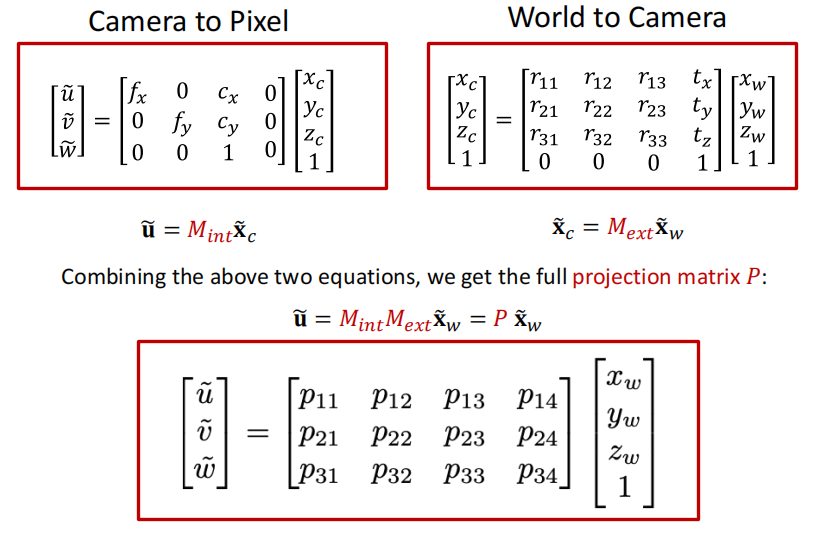
Camera calibration

1. Step 1: Capture an image of an object with known geometry. 如使用标定板作为已知世界坐标系

2. Step 2: Identify correspondences between 3D scene points and image points.

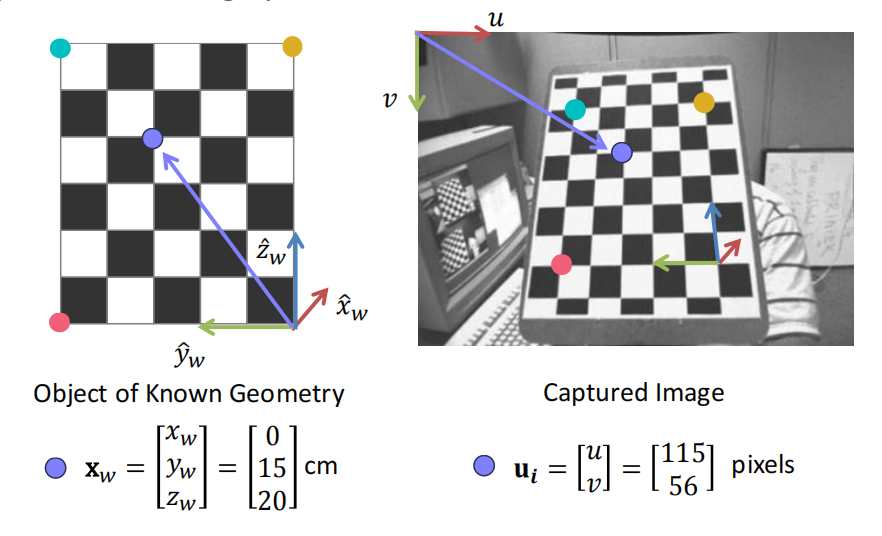
3. Step 3: For each corresponding point \(i\) in scene and image:

4. Step 4: Rearranging the terms

5. Step 5: Solve for \(p\)

   • 注意到对p的所有数同时乘除一个非零数不会影响结果
   • P is defined only up to a scale.
   • 因此我们通常定义最后一个分量为1或者p的模长为1
   • 我们让 \(Ap\) 尽可能为0，即\(\min\limits_{p}||Ap||^2\)同时使得 \(||p||^2=1\)
   • 可以知道解是矩阵\(A^TA\)最小特征值对应的特征向量

Decompose Projection Matrices to Intrinsic and Extrinsic Matrices

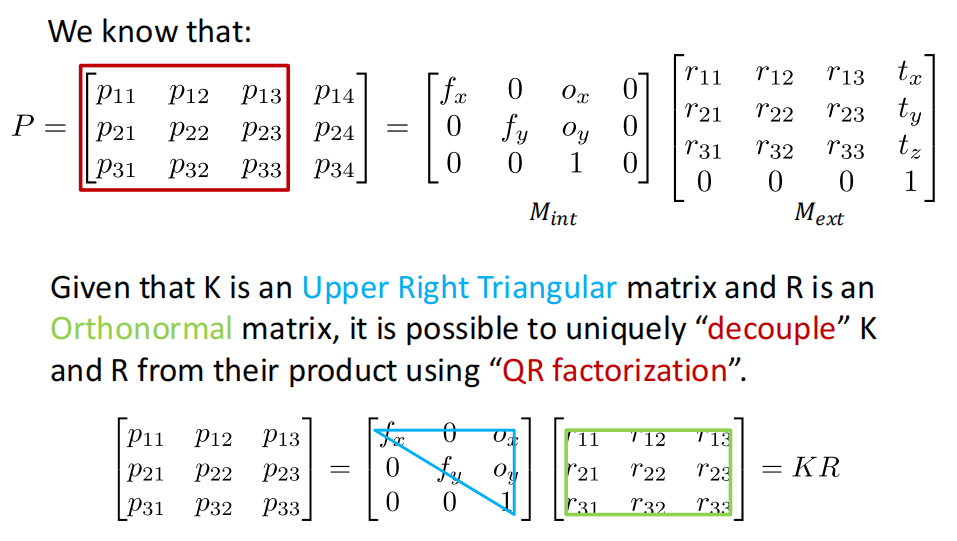
• 旋转矩阵是正交的，因为行列式值为1
• QR分解可以将一个矩阵分解成一个上三角矩阵和一个正交阵的乘积

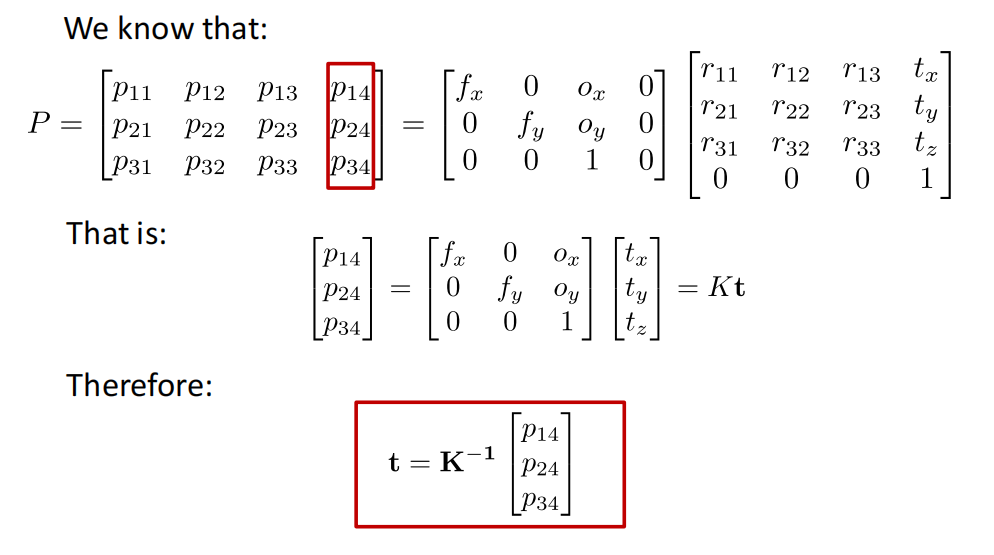
Perspective-n-Point problem

假设内参是固定的，只需要通过透视投影信息求出相机的位置和旋转

• 6 unknowns: 3 for rotation, 3 for translation
• Usually called 6DoF pose estimation

1. Direct Linear Transform (DLT) 需要6对点

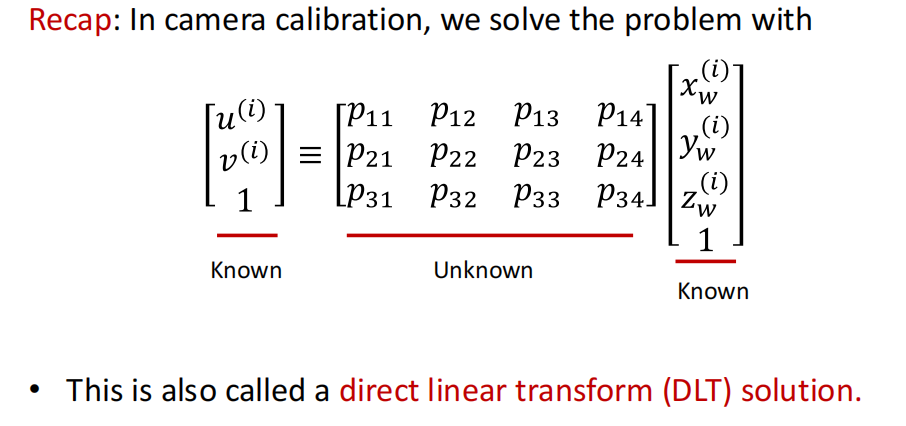
2. P3P: using the minimal number of points(3). 需要求解的只有OA, OB, OC，转化后即x,y

• 这个二元二次方程有四个可能解，我们使用一个额外的点去决定哪个解最有可能

3. A more general solution for PnP problem: mminimizing the reprojection error 重投影误差. \(p_i\)为given 2D points，后半部分式子为3D points投影到2D

\[ \min_{R,t}\sum_i\|p_i-K(RP_i+t) \|^2 \]

Structure from motion

Solving SfM

1. Assume intrinsic matrix \(K\) is known for each camera
2. Find a few reliable corresponding points
3. Find relative camera position \(t\) and orientation \(R\)
4. Find 3D position of scene points

Epipolar Geometry

对极几何描述了两个摄像机拍摄同一场景时，图像之间的几何关系。

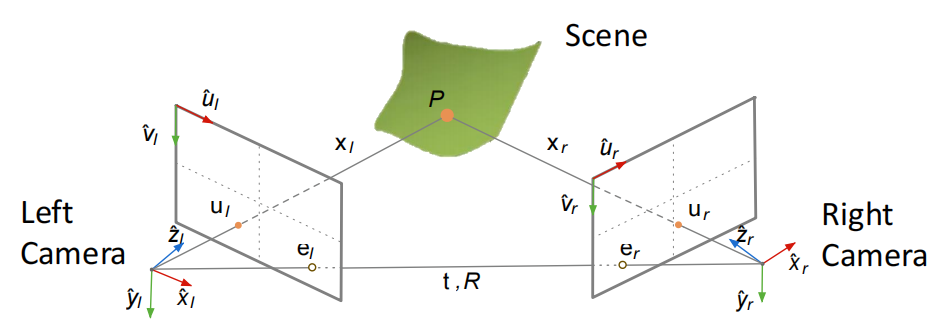
1. Epipole(极点)： Image point of origin/pinhole of one camera as viewed by the other camera.两个相机光心连线与图像平面的交点，相当于另一个相机在这个相机的投影位置

   • \(e_l\) 和 \(e_r\) 是对极点。给定相机时是唯一的。

2. Epipolar Plane of Scene Point \(P\): The plane formed by camera origins(\(O_l\) and \(O_r\)), epipoles(\(e_l\) and \(e_r\)) and scene point \(P\).

   • 场景中的每个点都位于唯一的极平面上

3. Epipolar Constraint

\[ x_l \cdot (t\times x_l)=0 \]

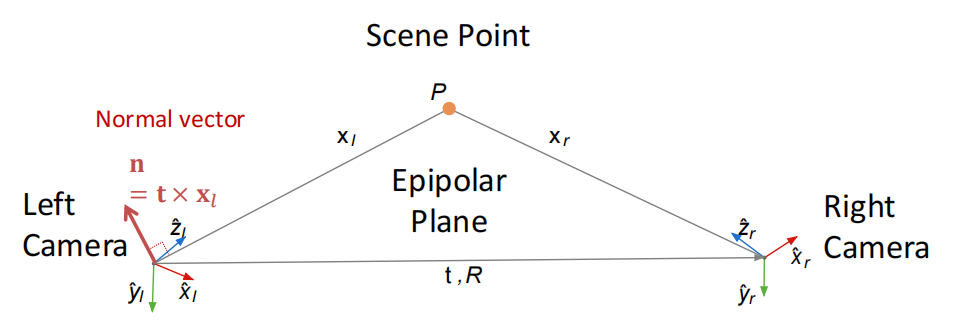
• We know \(x_l=Rx_r+t\)，用这个替代右侧的\(x_l\)，其中\(R\)和\(t\)是两个相机相对旋转和位置

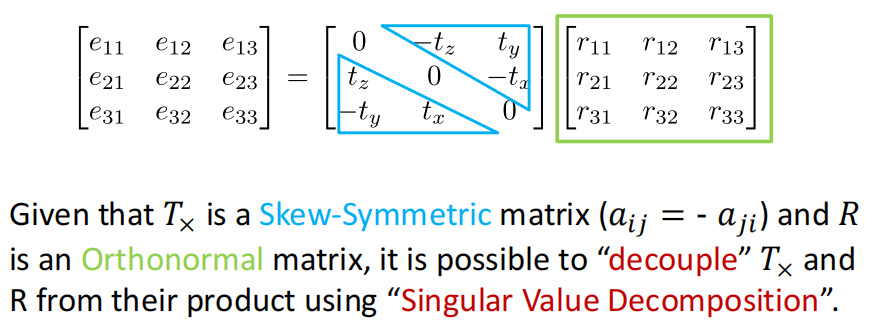
• 求出\(E\)就可以计算得到\(t\)和\(R\)

• find E: \(x_l^TEx_r=0\)

• depth of the scene points doesn't affect the epipolar constraint

• 我们把中间三个矩阵记作\(F\)，即Fundamental Matrix，则\(E=K_l^TFK_r\)

• \(F\)同样up to a scale，是尺度不变的，通常我们添加约束\(\|f\|^2=1\)

• 每一对点对应一个线性方程 由于有约束，需要8对点即可

• Step D: 计算\(E\)
• Step E: 分解得到\(R\)和\(t\)

Triangulation

Given corresponding 2D feature points and camera parameters, how to find the 3D coordinates of scene points? 给定两个相机的2D坐标和相机的外参内参，如何得到点在相机坐标系的坐标

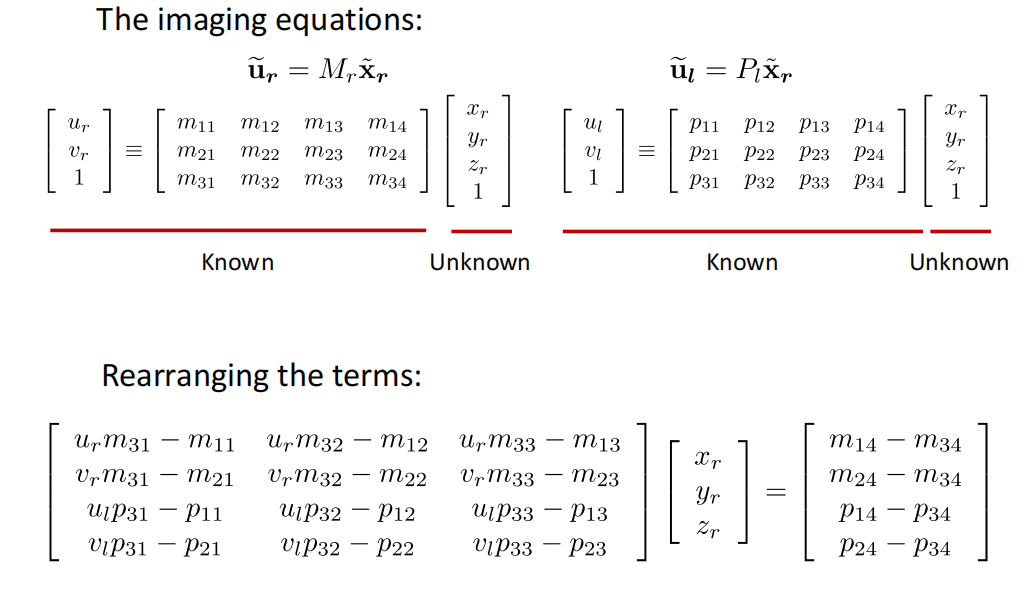
• 以上\(Ax_r =b\), Find least squares solution by \(x_r=(A^TA)^{-1}A^Tb\)

• triangulation by optimization

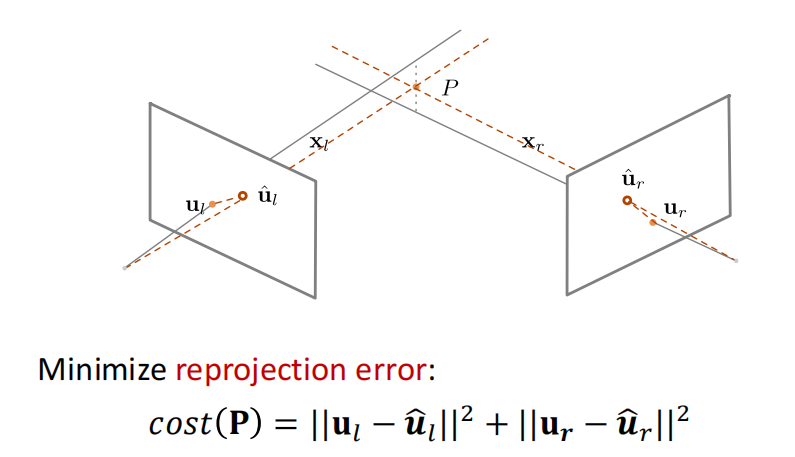
• Multi-frame Structure from Motion

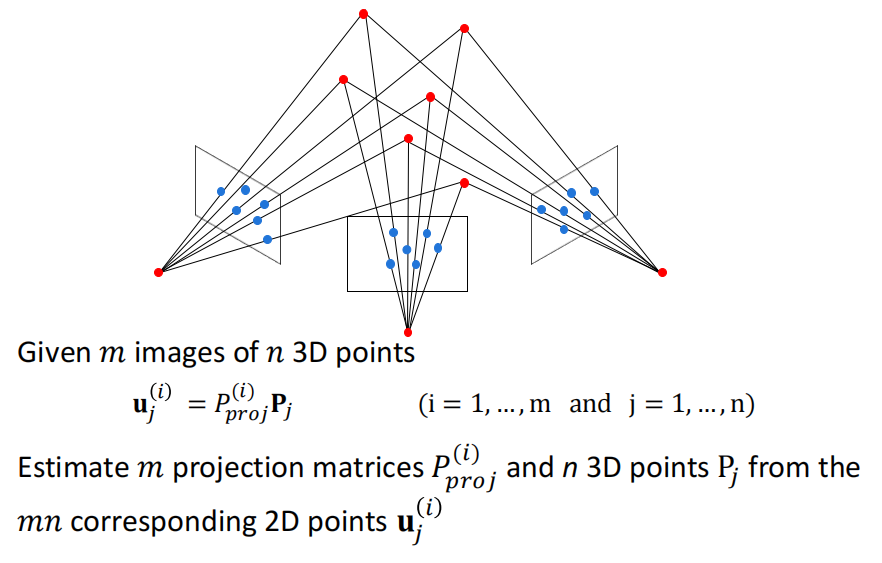
Sequential Structure from Motion

1. Initialize camera motion and scene structure

2. For each additional view

   • Determine projection matrix of new camera using all the known 3D points that are visible in its image
   • Refine and extend structure: compute new 3D points, reoptimize existing points that are also seen by this camera
   • 会出现累计误差
     • 可以采用回环检测
   

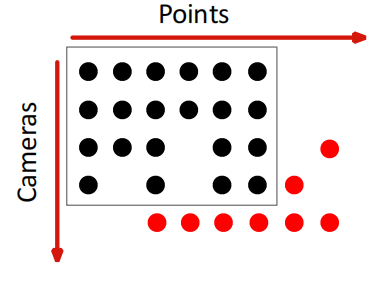
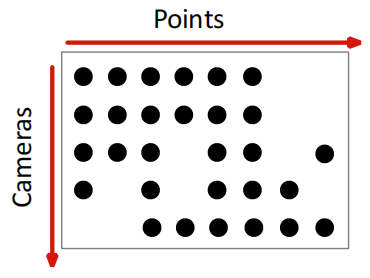
3. Refine structure and motion: Bundle Adjustment

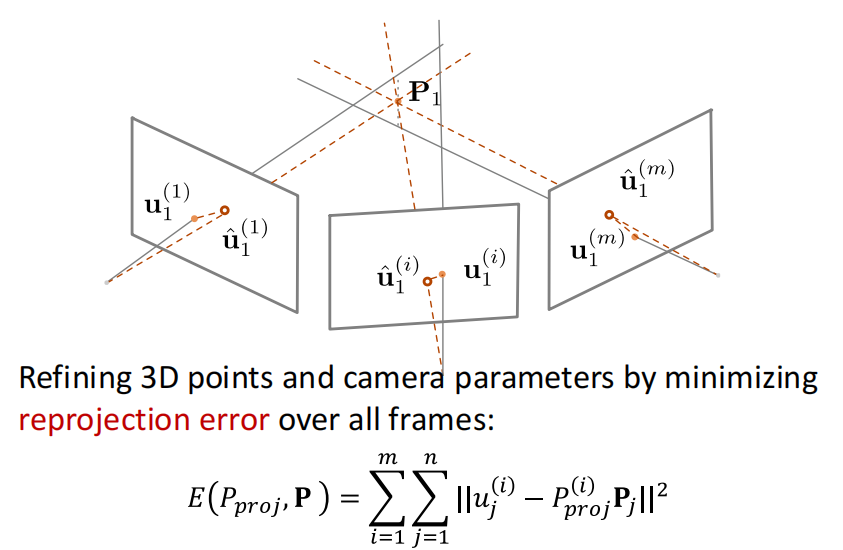
Incremental SfM pipeline

评论