Lec.06: Image stitching

Image Warping

1. parametric(global) warping: 所有像素点遵循统一的变换, \(p'=T(p)\)

2. projective transformation(Homography 单应变换): 透视投影、变换

   • 自由度为8，因为齐次坐标系下放缩没有影响，我们通常约束\([h_{00}\ h_{01}\dots h_{22}]\)的长度为1

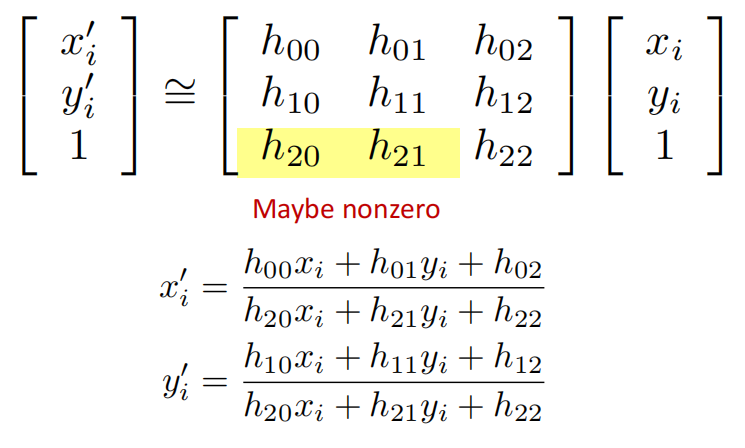
1. Change projection plane

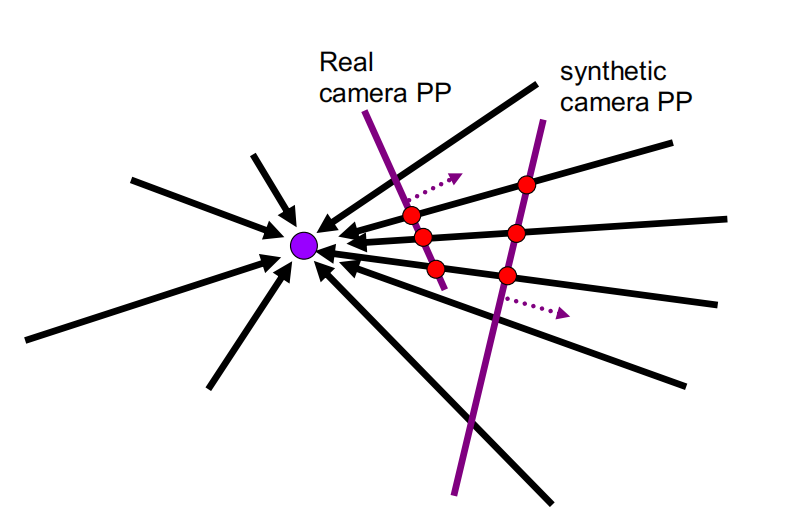
4. 什么时候是单应变换

   • 相机绕其中心转动
   • 相机中心移动并且拍摄内容在一个平面上

5. Inverse Transform(\(T^{-1}\)): 将变换图片每个像素点通过逆变换映射到原图的对应的位置，若坐标不为整数则利用插值得到对应像素

Image Stitching

1. Affine transformation

   \[ \left[\begin{array}{c}x'\newline y'\newline 1\end{array}\right]=\left[\begin{array}{ccc}a&b&c\newline d&e&f\newline 0&0&1\end{array}\right]\left[\begin{array}{c}x\newline y\newline 1\end{array}\right]=\left[\begin{array}{c}ax+by+c\newline dx+ey+f\newline 1\end{array}\right] \]
   • for each match
   \[ x^{\prime}=ax+by+c\newline y^{\prime}=dx+ey+f \]
   • for \(n\) matches
   \[ \left[\begin{array}{cccccc}x_1&y_1&1&0&0&0\newline 0&0&0&x_1&y_1&1\newline x_2&y_2&1&0&0&0\newline 0&0&0&x_2&y_2&1\newline &&\vdots&&&\newline x_n&y_n&1&0&0&0\newline 0&0&0&x_n&y_n&1\end{array}\right]\left[\begin{array}{c}a\newline b\newline c\newline d\newline e\newline f\end{array}\right]=\left[\begin{array}{c}x_1'\newline y_1'\newline \newline x_2'\newline y_2'\newline \newline \vdots\newline x_n'\newline y_n'\end{array}\right] \]

   • solve \(t\): find \(t\) that minimizes $$ |At-b |^2 $$

   • solution is given by $$ A^TAt=A^Tb t=(A^TA)^{-1}A^Tb $$

2. projective transformations

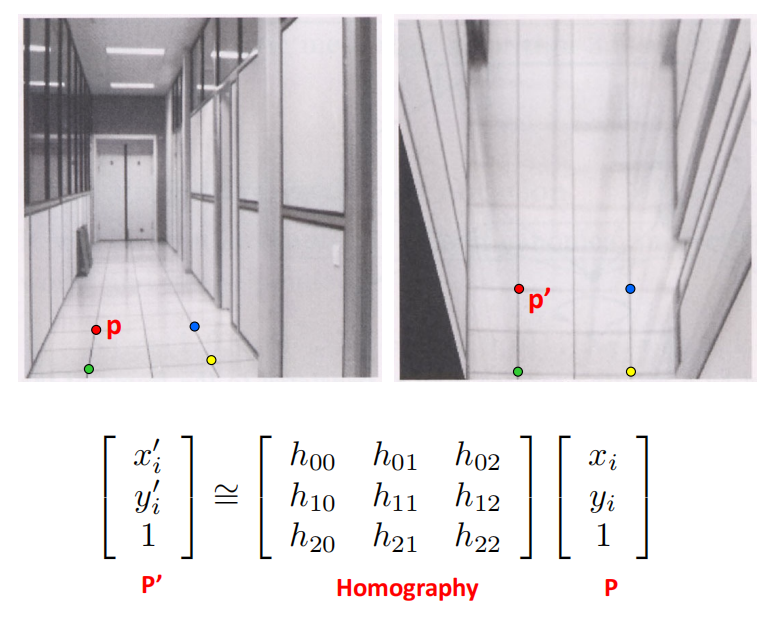
• solving for homographies

$$ x_i'\left(h_{20}x_i+h_{21}y_i+h_{22}\right)=h_{00}x_i+h_{01}y_i+h_{02} $$

$$ y_i'\left(h_{20}x_i+h_{21}y_i+h_{22}\right)=h_{10}x_i+h_{11}y_i+h_{12} $$

$$ \left[\begin{array}{cccccccc}x_i&y_i&1&0&0&0&-x_i'x_i&-x_i'y_i&-x_i'\newline 0&0&0&x_i&y_i&1&-y_i'x_i&-y_i'y_i&-y_i'\end{array}\right]\left[\begin{array}{c}h_{00}\newline h_{01}\newline h_{02}\newline h_{10}\newline h_{11}\newline h_{12}\newline h_{20}\newline h_{21}\newline h_{22}\end{array}\right]=\left[\begin{array}{c}0\newline 0\end{array}\right] $$

1. RANSAC

   • Idea: All the inliers will agree with each other on the translation vector; The outliers will disagree with each other

     • RANSAC only has guarantees if there are <50% outliers

   • General version:

     1. Randomly choose \(s\) samples - Typically \(s\) = minimum sample size that lets you fit a model

     2. Fit a model (e.g., transformation matrix) to those samples

     3. Count the number of inliers that approximately fit the model
     4. Repeat \(N\) times
     5. Choose the model that has the largest set of inliers
     6. final step: least squares fit: Find average translation vector over all inliers

2. Cylindrical projection 为了做360度的拼接

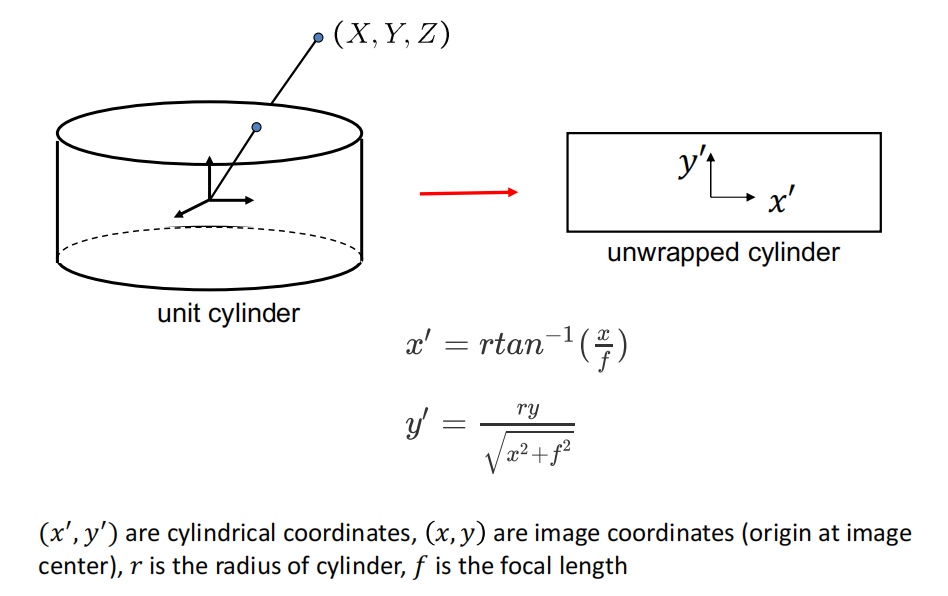
5. Cylindrical panoramas

   • step
     • reproject each image onto a cylinder
     • blend
     • Cylindrical image stitching: A rotation of the camera is a translation of the cylinder!
   • problem: Drift
     • small errors accumulate over time
     • solution: apply correction so that sum=0 for 360° pan

评论