Lec.05: Image Matching and Motion Estimation

Image matching

1. Main Components of Feature matching

   • Detection: identify the interest points
   • Description: extract vector feature descriptor surrounding each interest point
   • Matching: determine correspondence between descriptors in two views

Detection

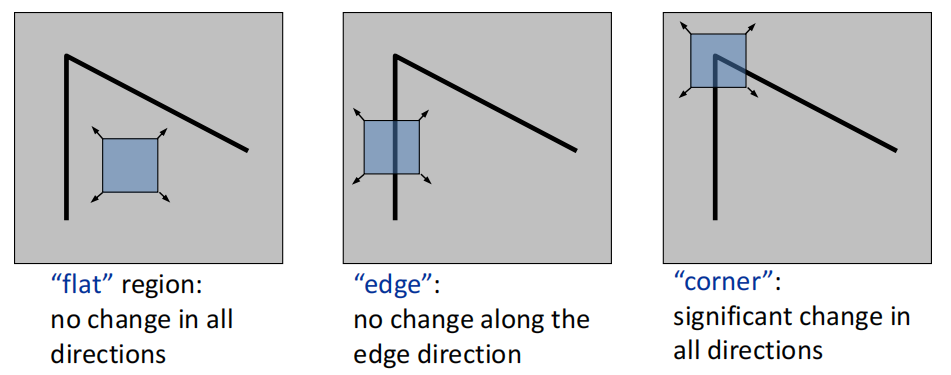
1. local measures of uniqueness: consider a small window of pixels (region), shifting the window in any direction causes a big change

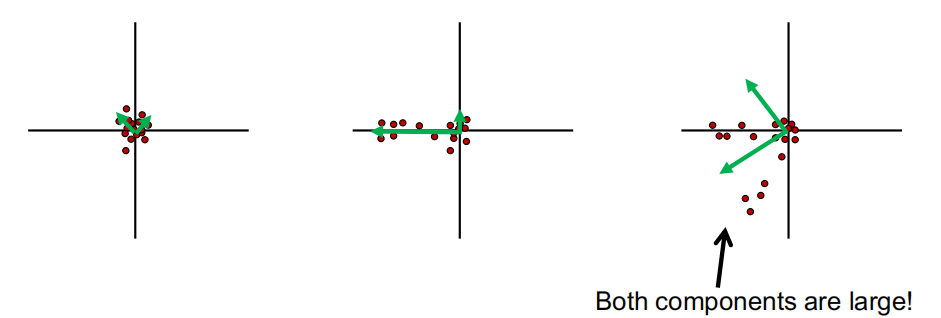
2. Principal Component Analysis

   • The 1^st principal component is the direction with highest variance.
   • The 2^nd principal component is the direction with highest variance which is orthogonal to the previous components.

1. Corner detection

   • Compute the covariance matrix at each point。\(w\)为高斯权重，即越中心权重越高

   $$ H=\sum_{(u,v)}w(u,v)\left[\begin{array}{cc}{I_{x}^{2}}&{I_{x}I_{y}}\newline {I_{x}I_{y}}&{I_{y}^{2}}\newline \end{array}\right]\quad I_{x}=\frac{\partial f}{\partial x},I_{y}=\frac{\partial f}{\partial y} $$

   • 二维情况下特征值有解析解 $$ H=\begin{bmatrix}a b\newline c d\end{bmatrix}\quad\lambda_{\pm}=\frac{1}{2}\left((a+d)\pm\sqrt{4bc+(a-d)^{2}}\right) $$

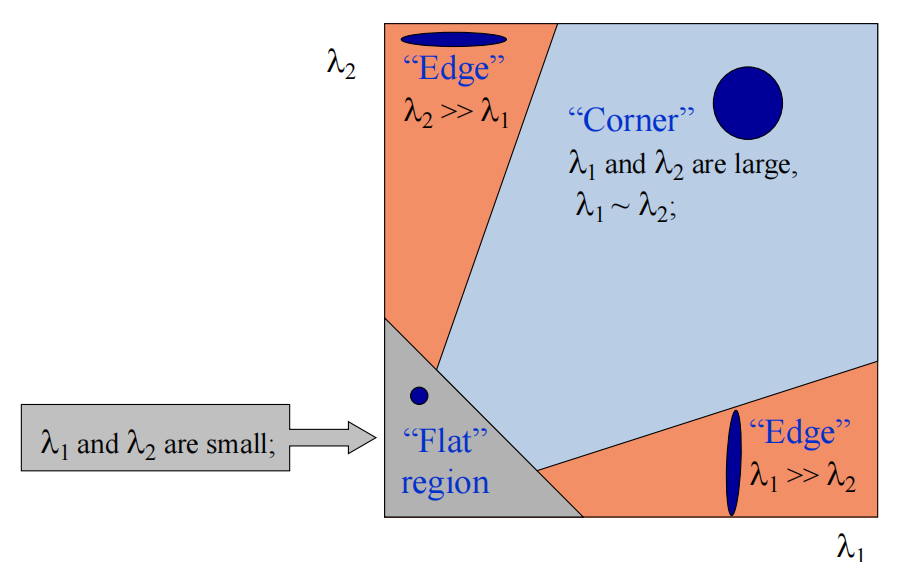
   • Classify points using eigenvalues of \(H\)

   • 简化，我们可以使用Harris operator。通过设置threshold进行二值化。最后找到response function的局部最大值 $$ f=\frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}=\frac{determinant(H)}{trace(H)} $$

2. Harris detector - Compute derivatives at each pixel - Compute covariance matrix \(H\) in a Gaussian window around each pixel - Compute corner response function \(f\) - Threshold \(f\) - Find local maxima of response function (nonmaximum suppression)

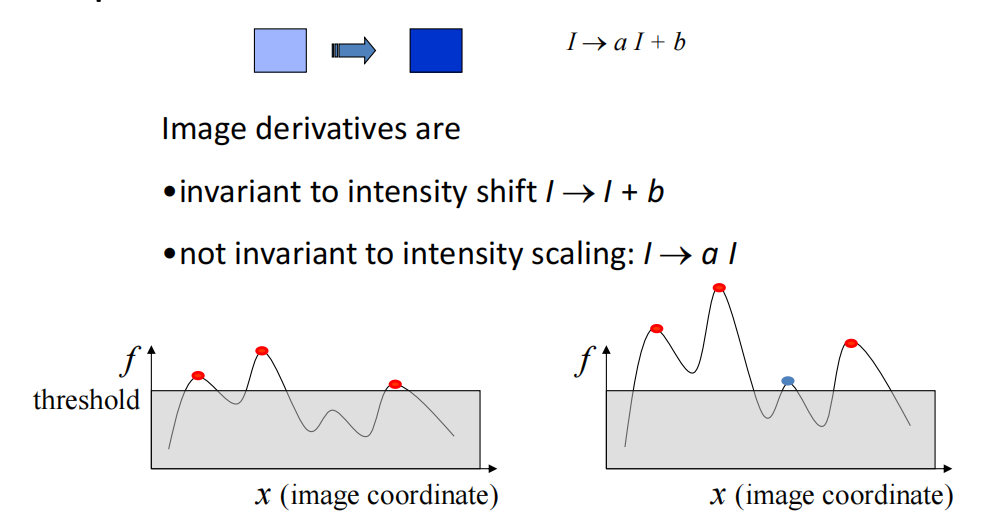
3. 特征点的可重复性: We want response value \(f\) at the corresponding pixels to be invariant to image tran sformations

   • Intensity change(亮度):极值会变，极值点不会, partially invarient
   

   • 平移、旋转: 不变

   • 缩放：corner response对缩放不是invariant的。

   • 对仿射变换和非线性亮度变换也不是不变的

     
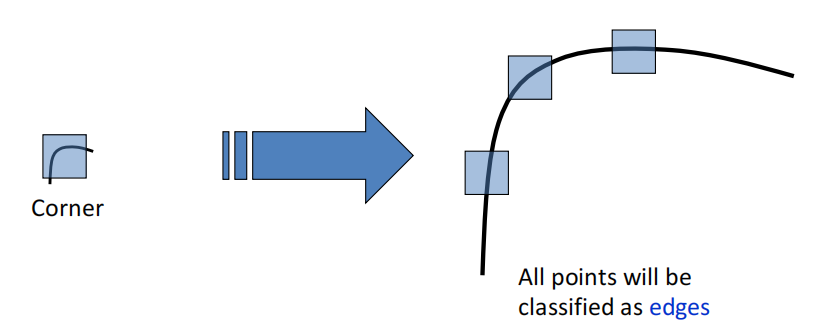
     • solution：在不同窗口大小下计算
     • implementation: Instead of computing \(f\) for larger and larger windows, we can implement using a fixed window size with an image pyramid

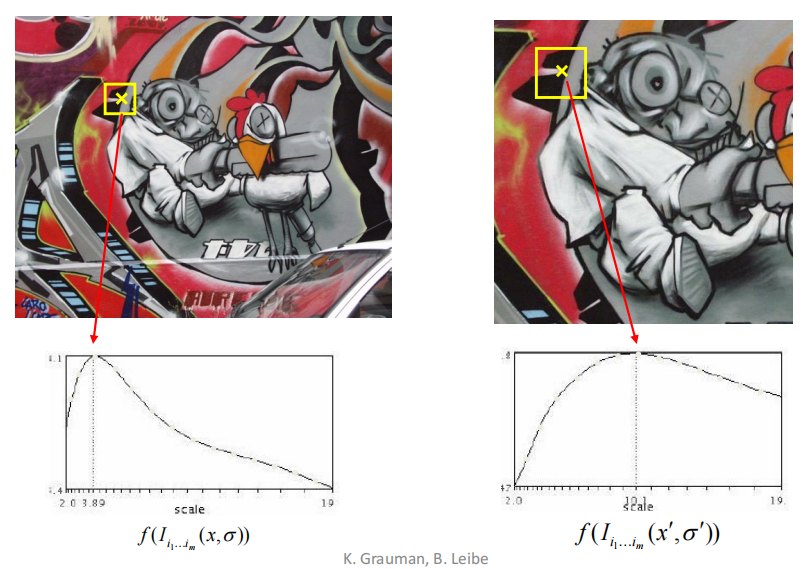
1. Blob detector:斑点在亮度图中二阶导值较大

   • Laplacian filter

     • \(\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\)
     • 近似
     
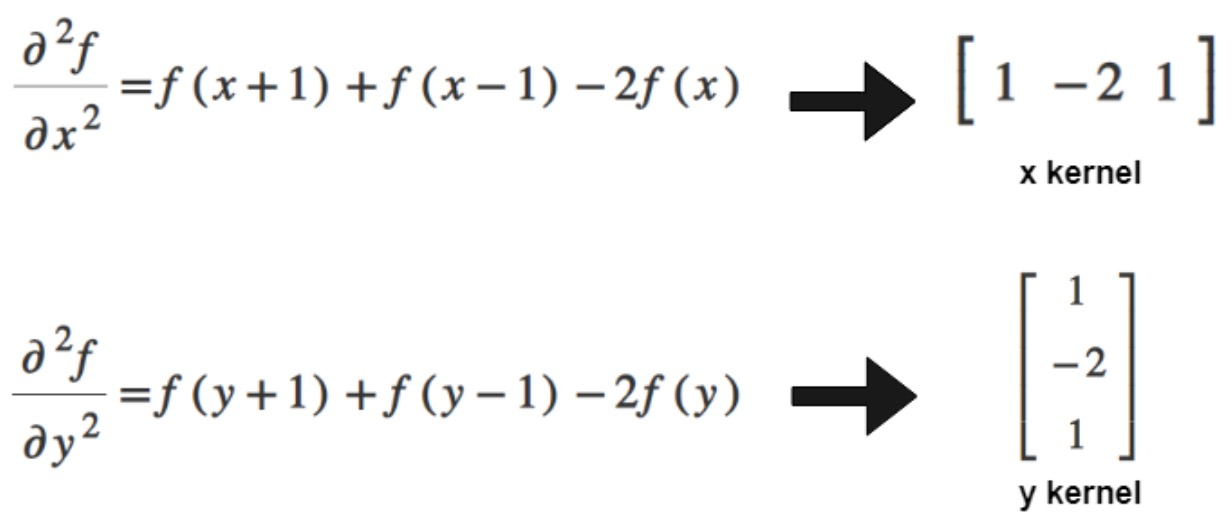
     • 加起来得到Laplacian filter

   • Laplacian对noise敏感，通常使用Laplacian of Gaussian(LoG) filter，利用高斯核smooth image

     • implementation: \(\nabla^2(f*g)=f*\nabla^2g\)​, \(g\)​ 为2D Gaussian function. The scale of LoG is controlled by \(\sigma\) of Gaussian

   • Scale selection: Feature points are local maxima in both position and scale. 把scale作为第三维度

   

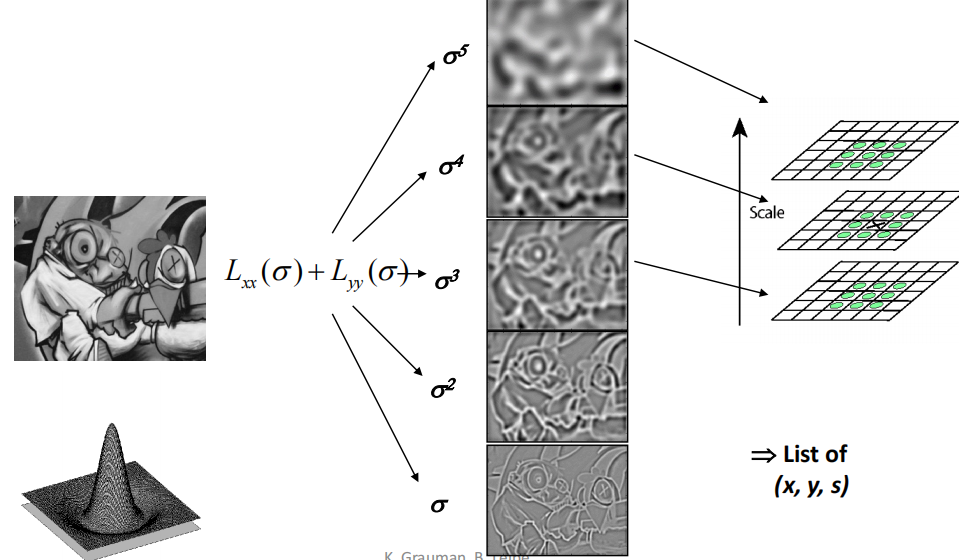
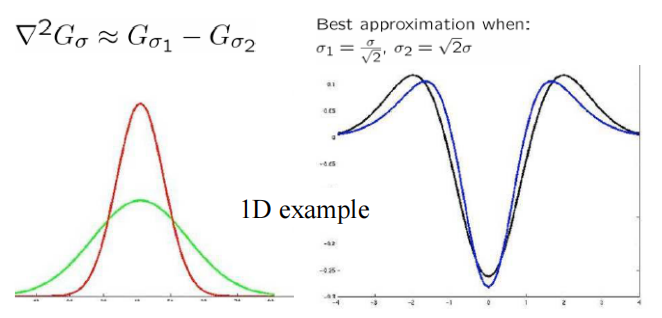
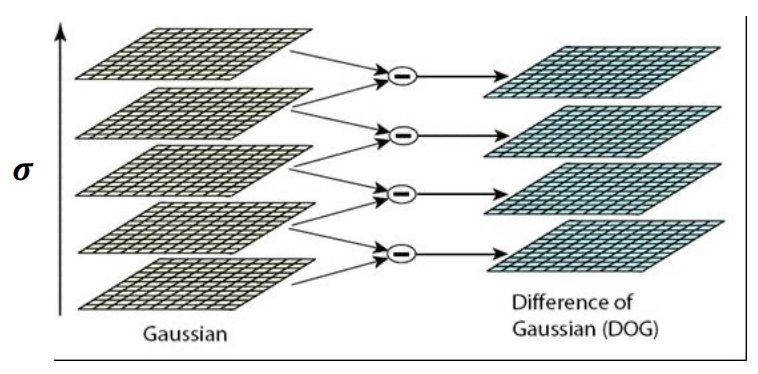
2. DoG: LoG can be approximated by Difference of two Gaussians (DoG) OpenCV中常用

   • computing DoG at different scales 在图像金字塔中对不同\(\sigma\)相减就可以得到不同scale下的DoG

Description

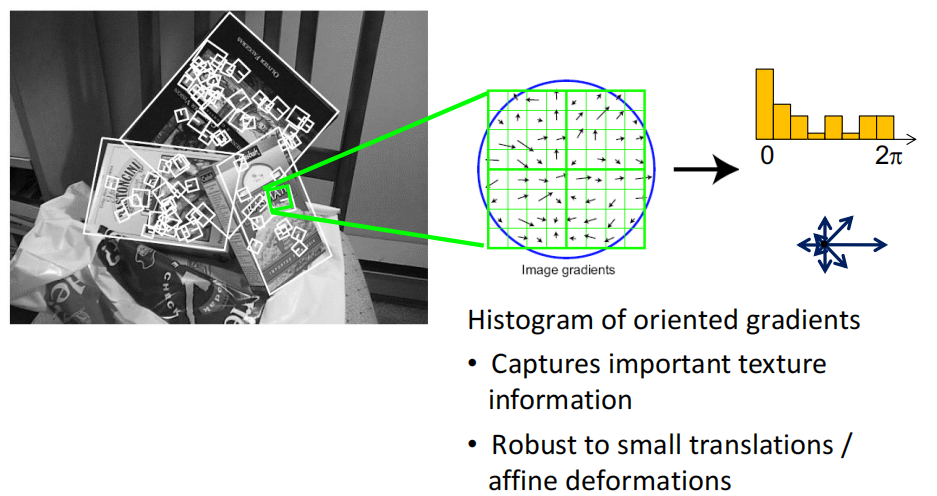
1. SIFT(Scale Invarient Feature Transform) descriptor:考察region内梯度方向的分布，用直方图作为描述子

   • 平移不发生变化
   • 旋转柱状图整体平移。处理：归一化，最大的放最左侧
   • 缩放：窗口大小由DoG detector检测特征点时决定，因此invariant
   • algorithm：DoG找到maxima，对旋转进行dominate orientation，最后create descriptor

1. Properties of SIFT: Extraordinarily robust matching technique

   • Can handle changes in viewpoint: Theoretically invariant to scale and rotation
   • Can handle significant changes in illumination: Sometimes even day vs. night
   • Fast and efficient: can run in real time
   • Lots of code available

Matching

1. Feature distance:

   • simple approach \(\|f_1-f_2\|\), can give small distances for ambiguous (incorrect) matches
   • ratio test: ratio score = \(\dfrac{\|f_1-f_2\|}{\|f_1-f_2'\|}\)
     • \(f_2\)是best match, \(f_2'\)是2nd best match
     • 很接近1说明很近似，则不对此点进行匹配

2. Another strategy: find mutual nearest neighbors 即找到一对特征点，彼此互为图中最近似的点

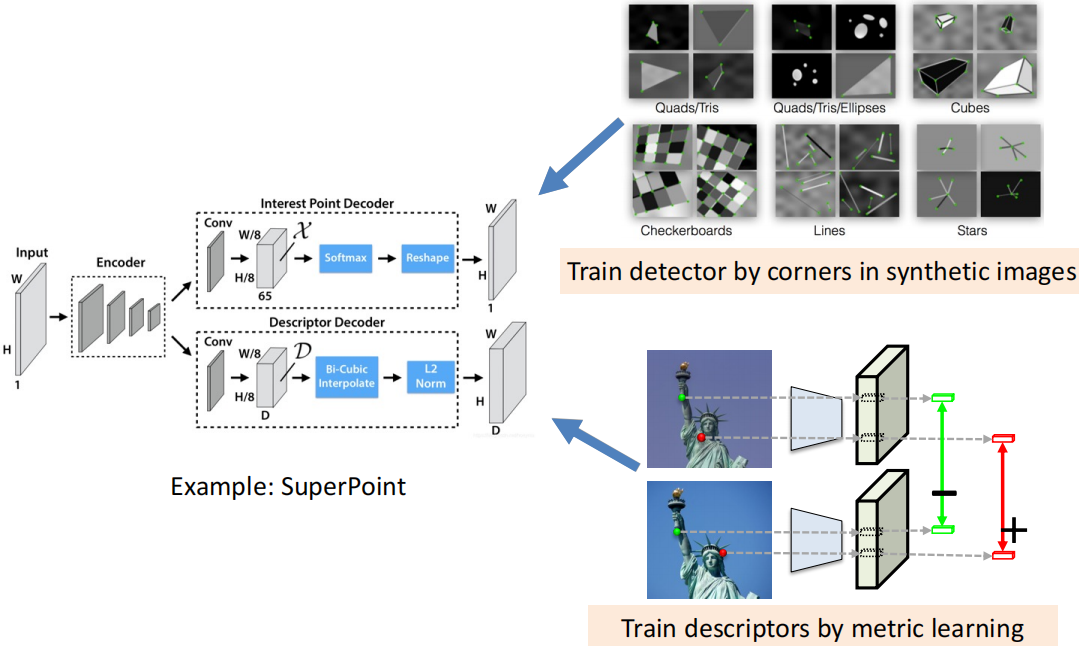
3. Deep Learning

Motion estimation

1. problem

   • feature-tracking: 提取追踪特征点，输出点的位移信息
   • optical flow：恢复每个像素处的图像运动，输出密集位移场（光流）

Lucas-Kanade method

1. Key assumptions

   • small motion: poitns do not move very far

   • brightness constancy: same point looks the same in every frame

     • \(I(x,y,t)=I(x+u,y+v,t+1)\)
     • Taylor expansion assuming small motion
     • 这样1个方程，但是有2个参数，我们需要更多的方程，就有了第三个假设
     

   • spatial coherence: points move like their neighbors

     • assume the pixel's neighbors have the same \((u,v)\)
     • for \(5\times5\) window, that gives us 25 equations per pixel
     \[ \left.\left[\begin{array}{cc}I_x(\mathbf{p_1})&I_y(\mathbf{p_1})\newline I_x(\mathbf{p_2})&I_y(\mathbf{p_2})\newline \vdots&\vdots\newline I_x(\mathbf{p_{25}})&I_y(\mathbf{p_{25}})\end{array}\right.\right]\left[\begin{array}{c}u\newline v\end{array}\right]=-\left[\begin{array}{c}I_t(\mathbf{p_1})\newline I_t(\mathbf{p_2})\newline \vdots\newline I_t(\mathbf{p_{25}})\end{array}\right] \]
     • 即\(Ad=b\),方程个数远多于变量，很可能没解，因此solve \(\min\limits_d\|Ad-b\|^2\)
     • 即\((A^TA)d=A^Tb\)
     \[ \left[\begin{array}{cc}\sum I_xI_x&\sum I_xI_y\newline \sum I_xI_y&\sum I_yI_y\end{array}\right]\left[\begin{array}{c}u\newline v\end{array}\right]=-\left[\begin{array}{c}\sum I_xI_t\newline \sum I_yI_t\end{array}\right] \]

     • 有解左侧要可逆，对应两个特征值\(\lambda_1\)和\(\lambda_2\)不能太小，对应之前提到的边缘检测，需要是corner点

     • The aperture problem 无法判断沿孔径方向的运动

     

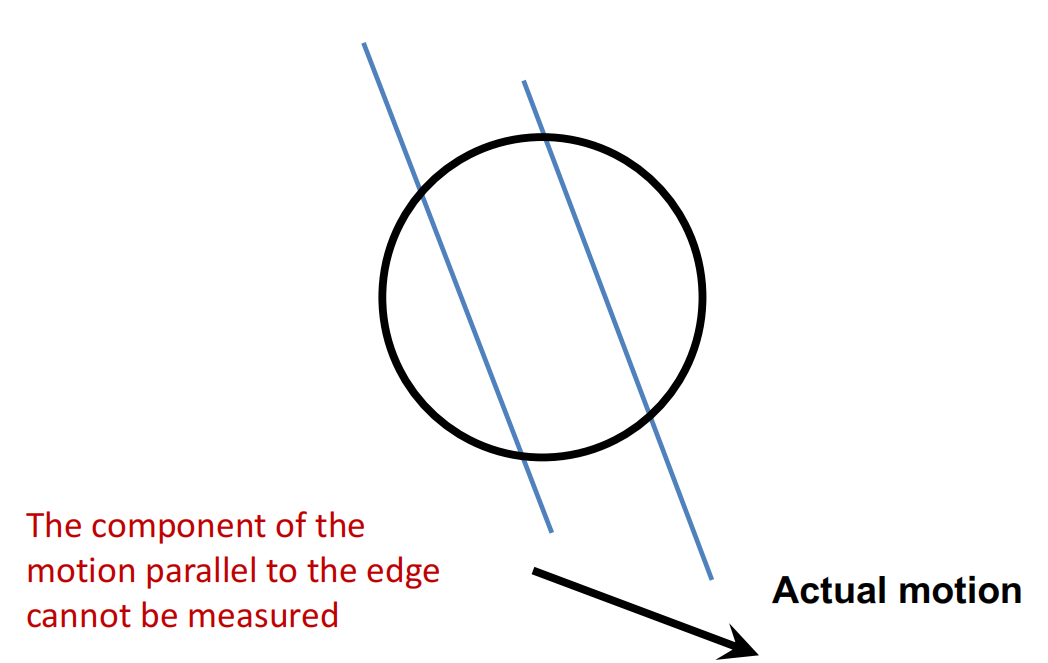
2. 好跟踪的点：纹理丰富的点

3. Errors in Lukas-Kanade

   • Brightness constancy is not satisfied 如开关灯、进出隧道

     • solution: 梯度是不变的

   • The motion is not small 跑步的人

     • solution: 降低分辨率, coarse-to-fine optical flow estimation
     

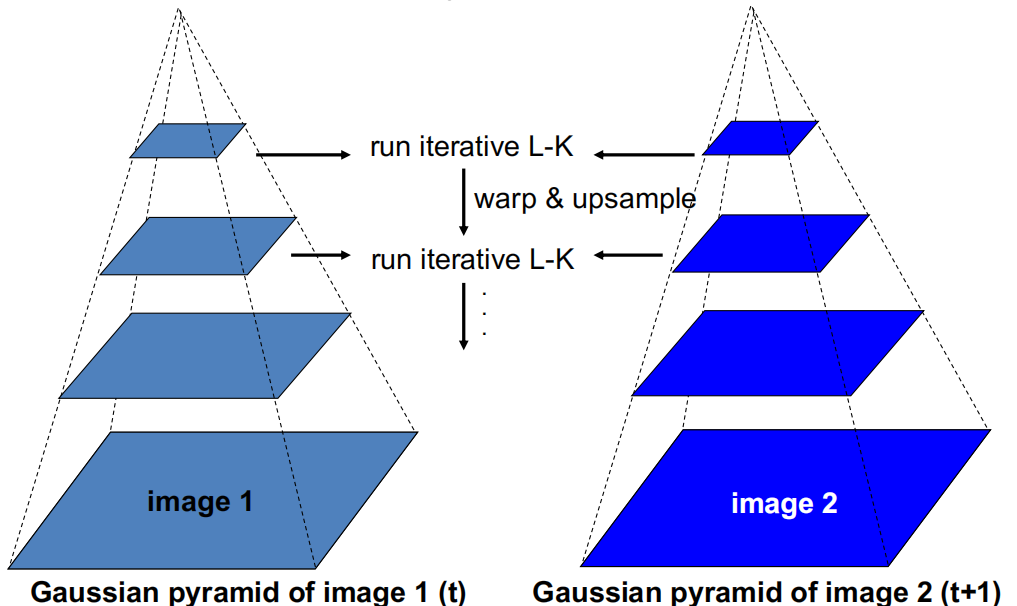
   • A point does not move like its neighbors 边缘

评论