跳转至

Lec.03: Image Processing

Image Processing Basics

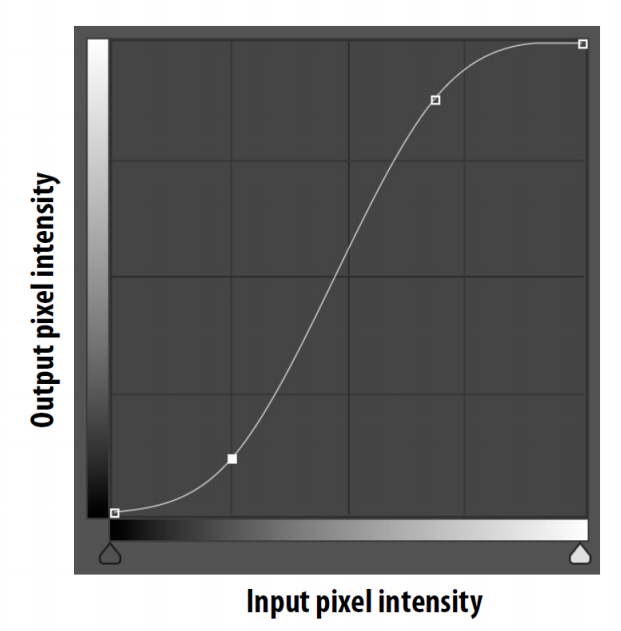
  1. increase contrast with 'S curve' \(\text{output}(x,y)=f(\text{input}(x,y))\)

    • S型，亮的更亮，暗的更暗，提高对比度
image-20240926105653055
  1. Convolution
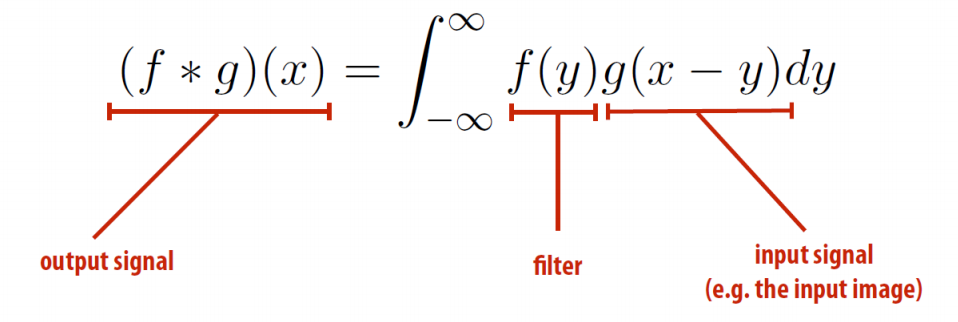
image-20240926110440691
  • Discrete 2D Convolution
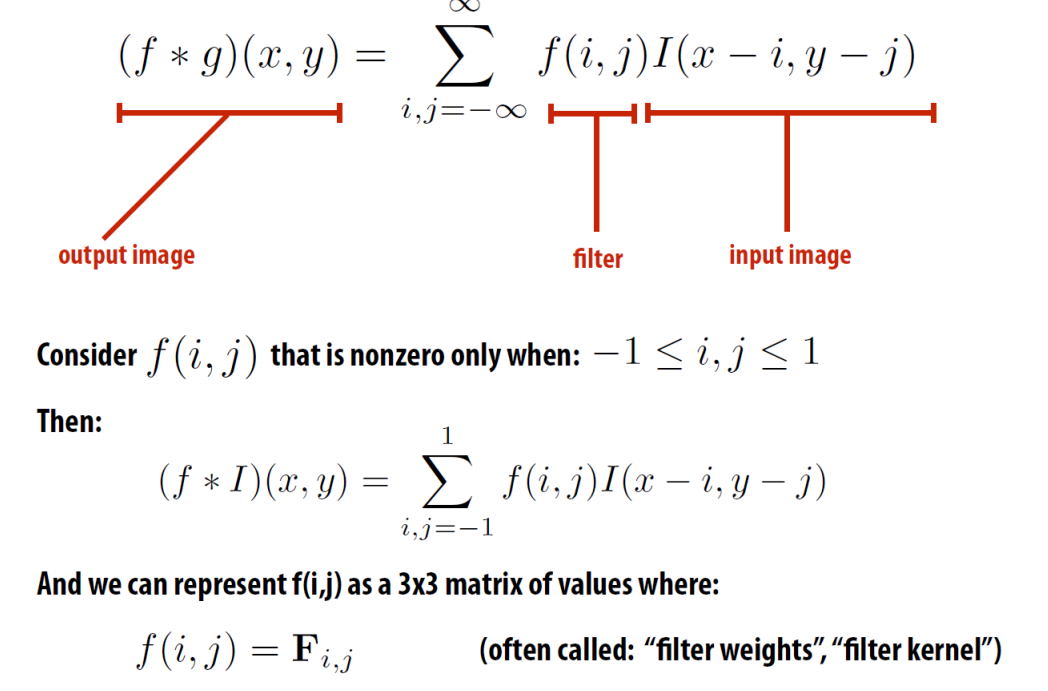
image-20240926110829808

  • Padding: add pixels around the image border, zero values, edge values, symmetric...

  • Gaussian Blur: \(f(i,j)=\dfrac1{2\pi\sigma^2}e^{-\dfrac{i^2+j^2}{2\sigma^2}}\)

  • \(\sigma\)大一些更糊

  • Sharpening

  • High frequencies in image \(I=I-blur(I)\)

  • Sharpened image \(=I+(I-blur(I))\)，即在原图添加高频部分

  • 边缘检测

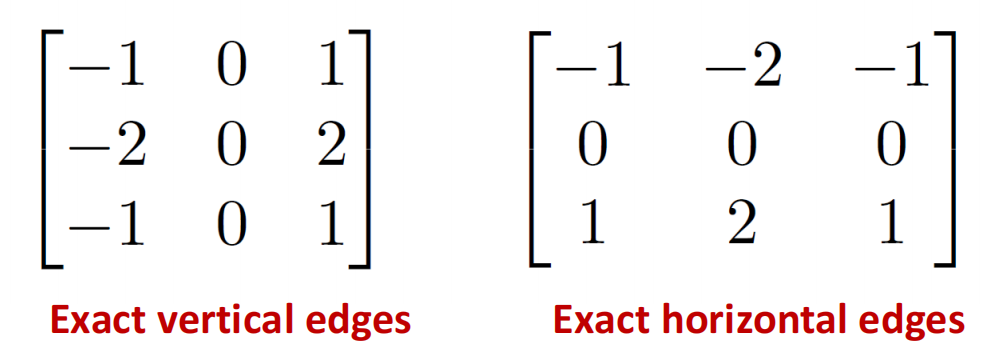
image-20240926112023823
  • 可以认为filter是对特定pattern的检测

Image Sampling

  1. Aliasing: artifacts due to sampling. Signals are changing too fast but sampled too slow
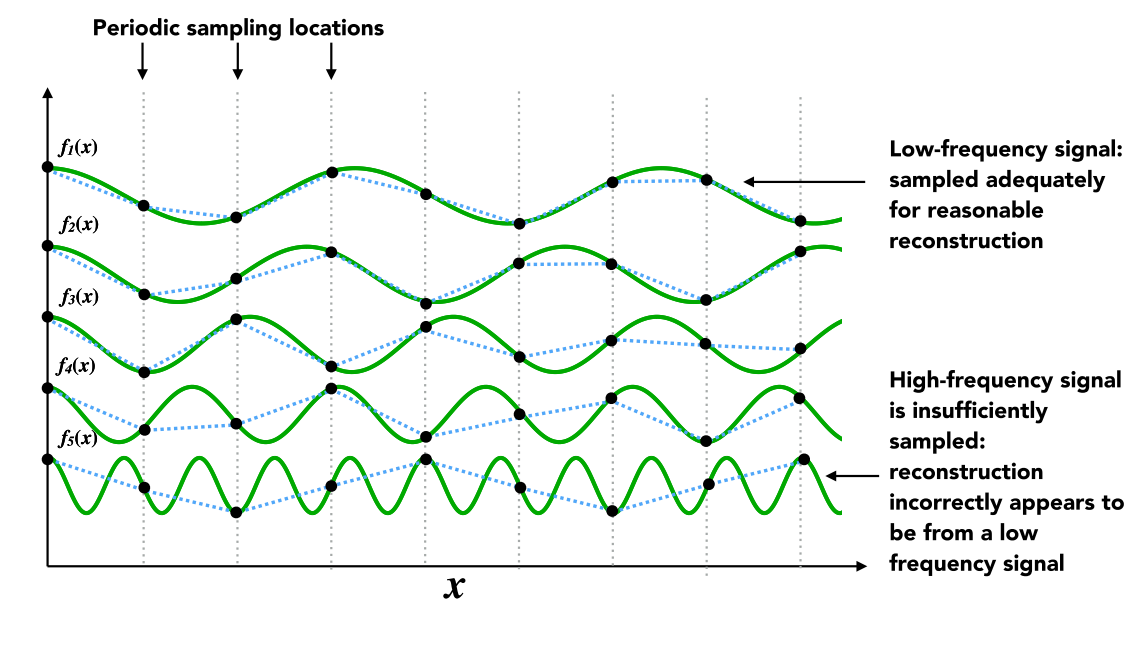
image-20240926113902574
  1. 把任意信号用正余弦信号表示 -> Fourier Transform
\[ \begin{aligned}&\bullet F(u)=\int_{-\infty}^{\infty}f(x)e^{-i2\pi ux} dx\newline &\bullet f(x)=\int_{-\infty}^{\infty}F(u)e^{i2\pi ux} du\newline &\bullet x{:}\mathrm{space},u{:}\mathrm{frequency},e^{i\theta}=cos\theta+isin\theta,\newline &i=\sqrt{-1}\end{aligned} \]
  • 高斯函数的傅里叶变换还是高斯函数

  1. Convolution Theorem：空间域和频域之间的关系

    • 空间域中的卷积操作等价于频率域中的逐点乘法操作
    • 应用卷积定理的步骤
      1. 计算傅里叶变换：将\(f(x,y)\)和\(g(x,y)\)通过二维傅里叶变换转换为\(F(u,v)\)和\(G(u,v)\)。
      2. 在频率域中相乘：计算乘积\(H(u,v)=F(u,v)\cdot G(u,v)\)。
      3. 逆傅里叶变换：将\(H(u,v)\)通过逆傅里叶变换转换回空间域，得到卷积结果\(h(x,y)\)。
image-20240926120233062
  1. box filter = low-pass filter 全是1
    • wider kernel = lower frequency
  2. 采样频率低，在频域脉冲密集，产生混叠，导致采样失真
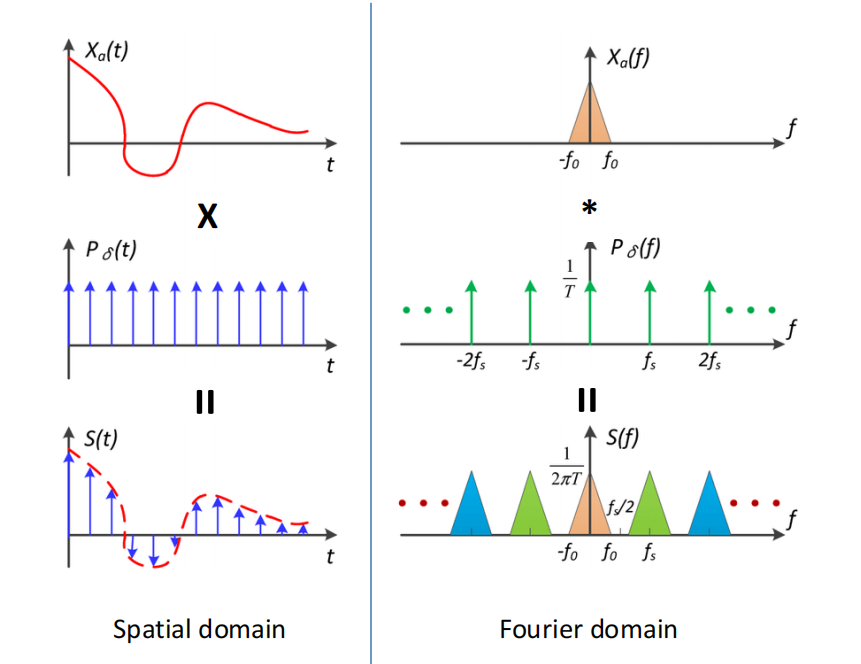
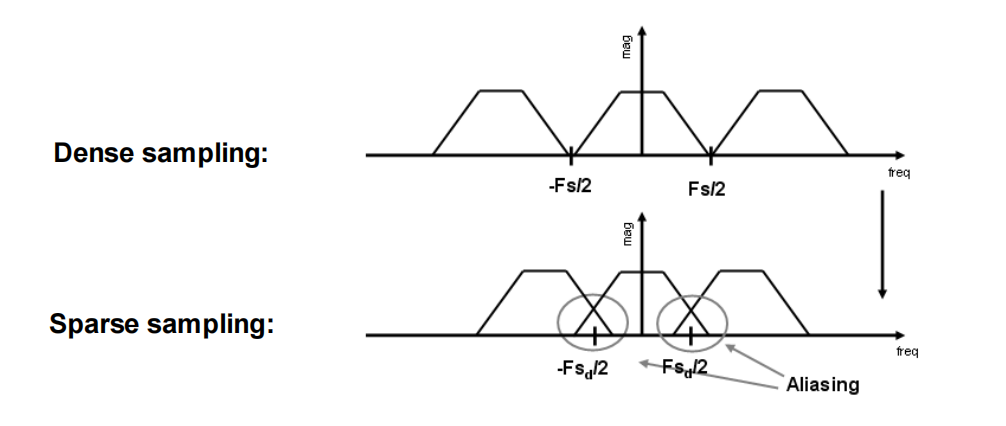
image-20240926121339953image-20240926121353411

  • 解决措施

  • 提高采样率 Nyquist-Shannon theorem: Consider a band-limited signal: has no frequencies above \(f_0\), the signal can be perfectly reconstructed if sampled with a frequency larger than \(2f_0\)

    important

  • Anti-aliasing: Filtering out high frequendcies before sampling

    1. Convolve the image with low-pass filters (e.g. Gaussian)

    2. Sample it with a Nyquist rate

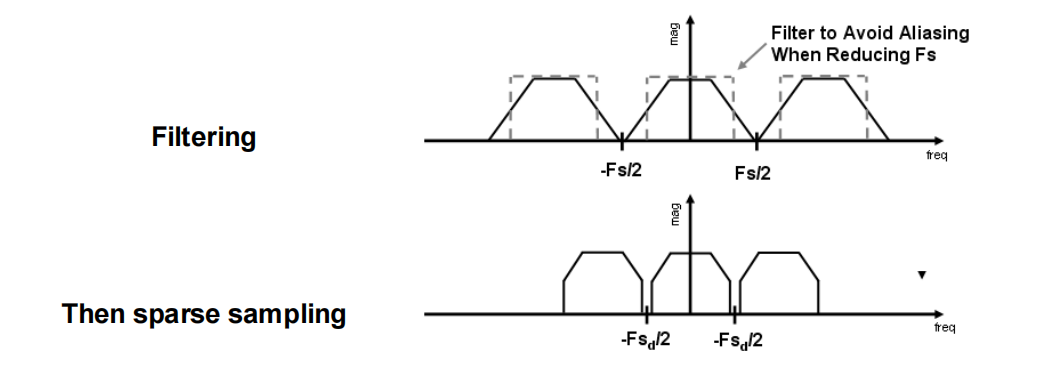
image-20240926121722339

Image Magnification

  1. 插值

    • Nearest-neighbor interpolation：不连续不平滑

    • Linear interpolation：连续，不平滑

    • Cubic interpolation：用三次曲线逼近，连续，平滑

    • Bilinear Interpolation

      • Generally bilinear is good enough

      image-20240926122503252

    • Bicubic Interpolation: \(p(x,y)=\sum_{i=0}^3\sum_{j=0}^3a_{ij}x^iy^j\)

Change Aspect Ratio

  1. Basic idea:

    • Problem statement: we need to remove \(n\) pixels from each row
    • Basic idea: remove unimportant pixels

  2. Importance of pixel

    • Edge energgy: \(E(I)=|\dfrac{\partial I}{\partial x}|+|\dfrac{\partial I}{\partial y}|\)
    • 计算：通过卷积

  3. Seam carving: Find connected path of pixels from top to bottom of which the edge energy is minimal。每次每行删除一个像素，要删除n个则跑n次

    • solved by dynamic programming:

      • If \(M(i,j)\) = minimal energy of a seam going through \((i,j)\)
      • Then
      \[ \mathbf{M}(i,j)=E(i,j)+\min\left(\mathbf{M}(i-1,j-1),\mathbf{M}(i-1,j),\mathbf{M}(i-1,j+1)\right) \]

  4. Seam insertion: Find \(k\) seams to insert, then interpolate pixels

评论