Chapter 3 Combinational Logic Design¶

Part 1 Implementation Technology and Logic Design¶

分层设计¶

原子模块(Primitive Block)：与门、或非、非门等等
分层设计：模块可重用性非常重要。先决条件：电路是规整(regularity)的
1. 分层设计即将复杂问题模块化为若干层次，之后逐个解决
2. 分为自顶向下和自底向上
3. 前者从需求开始，后者从现有模块开始
出现在设计中的模块被称为这个模块的一个实例（instance），将它应用称为实例化（instantiation）

集成电路¶

又叫做芯片，分为以下等级

SSI (small-scale integrated) 不到10个gate
MSI(medium-\(\cdots\)) 10-100个gates
LSI(large\(\cdots\))成百上千个gates
VLSI(very large) 成千上亿个gates

技术参数¶

Name	Description
Fan-in	一个门可用的输入
Fan-out	一个栅极输出驱动的标准负载数量
Logic Levels	被认为是高低电平的输入输出电压范围
Noise Margin	对外界噪声的容忍能力(具体来说是不会导致行为异变的最大噪声压值)
Cost for a gate	继承电路的门成本
Propagation Delay	信号改变后从输入到输出所需的变化时间
Power Dissipation	电源输出能耗和门的能耗

扇入扇出：扇入描述了一个门能够接受的最多输入量，如一个四输入与非门的扇入就是 4；而扇出描述的则是一个门的输出(栅极输出)在不降低工作性能的情况下能够负载多少门，例如一个非门的输出能够同时负载 4 个非门并且都能正常工作，则其扇出为 4，其也能通过标准负载来定义。
所谓的标准负载，是衡量“负载”的一个“单位砝码”。其大小等于一个非门(逆变器)贡献的负载压力。
转换时间：转换时间分为\(t_{LH}\)（rise time）和\(t_{HL}\)（fall time）两个部分
rise time 等于栅极输出从 \(V_{CC}\) 的 10% 升高到 90% 所需要的时间；
fall time 等于栅极输出从 \(V_{CC}\)的 90% 降低到 10% 所需要的时间；

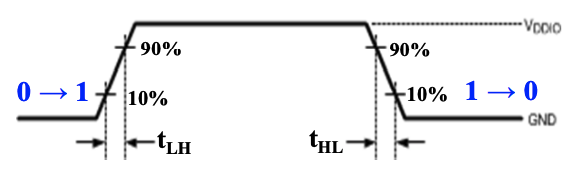
随着负载增加，转换时间也会增加（给电容充电的时间增加），而扇出定义中提到的“最大负载”，就是指它的转换时间不超过它预定的最大转换时间。

从左到右表示负载不断增加时，rise time 的变化趋势。
实际上，类似的，超出扇入后，门对输入的反应就太慢了。

工艺映射¶

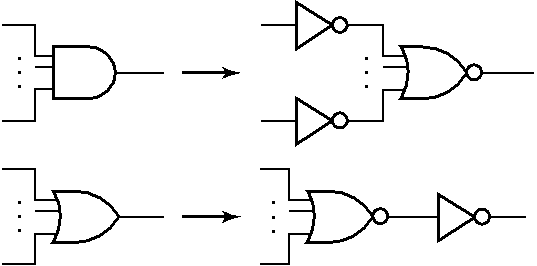
形式上：积之和形式使用与非门，和之积形式使用或非门

NAND Mapping Algorithm 与非门成本更低，延迟更低¶

Replace ANDs and ORs:
消除所有反相器对
Repeat the following pair of actions until there is at most one inverter between :
1. A circuit input or driving NAND gate output, and-
2. The attached NAND gate inputs.

NOR Mapping Algorithm¶

Similar to the NAND,first Replace ANDs and ORs

EN 使能¶

EN为0输出始终为0，EN为1时为对应表达式值

Part 2 Combinational Logic¶

Decoding 译码¶

Decoding - the conversion of an n-bit input code to an m-bit output code with\(n\leqslant m\leqslant2^n\) such that each valid code word produces a unique output code
Circuits that perform decoding are called decoders
Here, functional blocks for decoding are called n-to-m line decoders, where \(m\leqslant2^n\), and generate \(2^n\) (or fewer) minterms for the n input variables

3-8 译码器¶

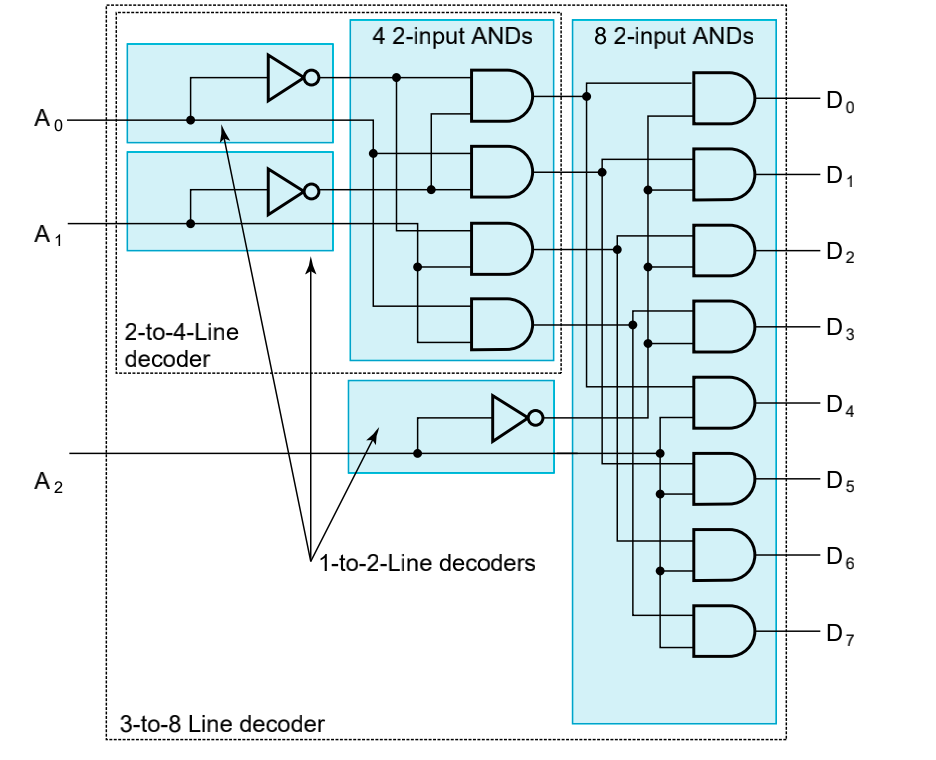
设计n输入译码器，不断二分，除不尽就剩下一个单独的，如上图3除2余1，因此我们使用1个4-2译码器和一个1-2-Line Decoder

通过译码器和OR可以组成任何组合逻辑电路

Decoder with Enable¶

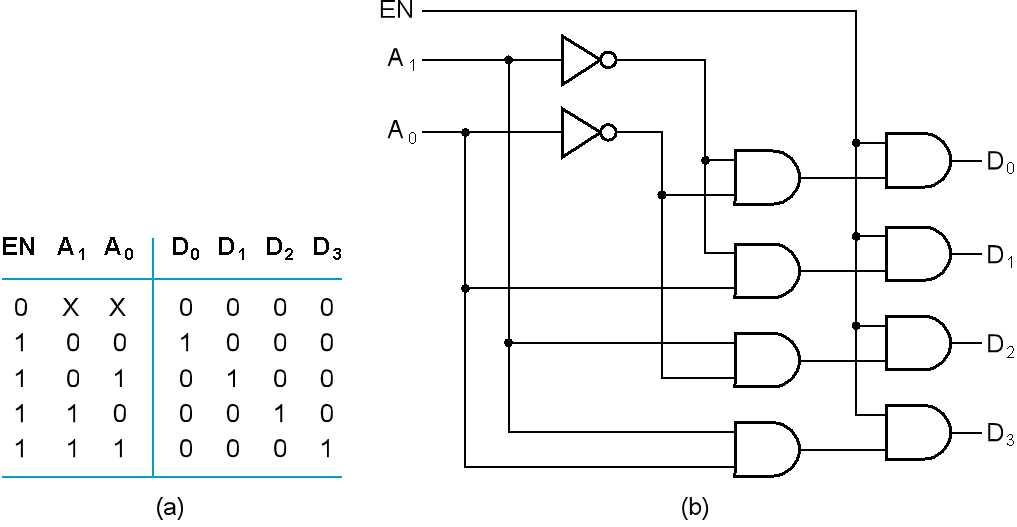
由于2-4译码器只有一个输出为1，只有该门可以输出内容，因此可以将\(A_1,A_0\)组成的译码器当成EN，EN当成输入信号

带使能输入的译码器又被称为多路分配器

基于译码器的组合电路¶

当F最小项个数超过\(\overline{F}\)最小项个数，函数取反可以用更少最小项表示

BCD-to-Segment Decoder¶

共阳极与共阴极接法：

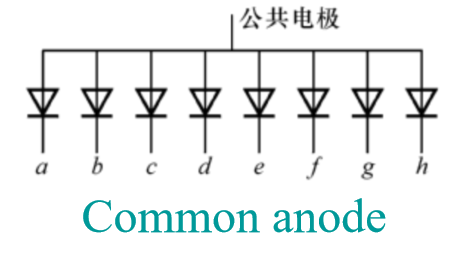
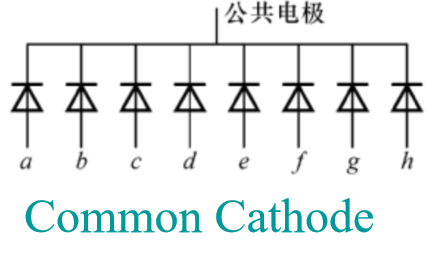
Encoding¶

Encoding - the opposite of decoding - the conversion of an m-bit input code to a \(n\)-bit output code with \(n < m< 2^n\) such that each valid code word produces a unique output code
An encoder has \(2^n\) (or fewer) input lines and \(n\) output lines which generate the binary code corresponding to the input values
传统编码器问题：如以下输出方程式对应编码器，若\(D_6,D_7\)同时为1，不能判断是\(A_2\)还是\(A_1\)，即有不确定性

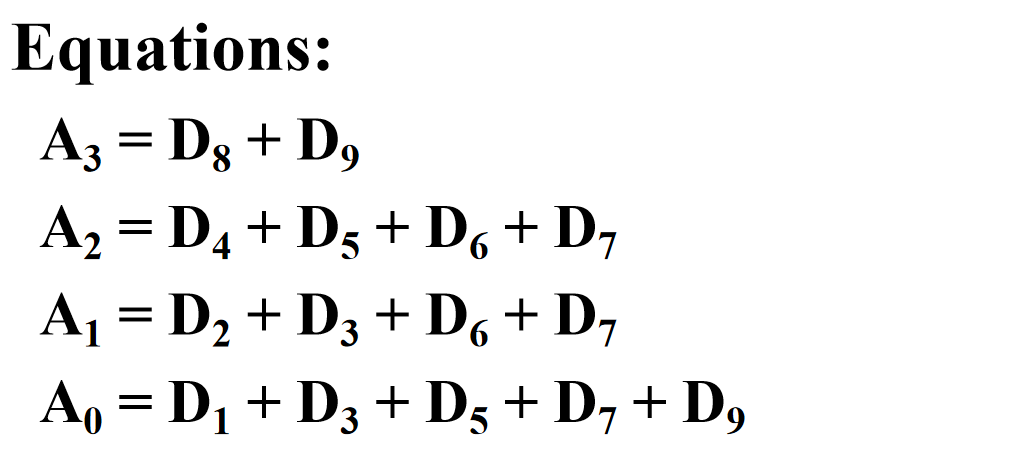
优先编码器（Priority Encoder）

位数越高优先级越高。增加一个单独输出V表示至少有一个输入为0以与\(D_0=1\)区分

  - One encoder that can accept all possible combinations of input values and produce a meaningful result is a priority encoder.
  - Among the 1s that appear, it selects the most significant input position (or the least significant input position) containing a 1 and responds with  the corresponding binary code for that position.
  - example:
    - Priority encoder with 5 inputs (D4, D3, D2, D1, D0) - highest priority to most significant 1 present - Code outputs A2, A1, A0 and V where V indicates at least one 1 present.
    - <div align="center"><img src="https://pixe1ran9e.oss-cn-hangzhou.aliyuncs.com/image-20231026111647111.png" alt="image-20231026111647111" style="zoom:50%;" /></div>
  - Xs in input part of table represent 0 or 1; thus table entries correspond to product terms instead of minterms. The column on the left shows that all 32 minterms are present in the product terms in the table
  - Xs 在输出列表示无关情况不同

Selecting¶

Selecting of data or information is a critical function in digital systems and computers
Logic circuits that perform selecting are called multiplexers
Selecting can also be done by three-state logic or transmission gates

Multiplexer 多路复用器 MUX¶

A multiplexer selects information from an input line and directs the information to an output line
typical multiplexer has n control inputs (\(S_{n-1}, … S_0\)) called selection inputs, \(2^n\) information inputs (\(I_{2^n - 1}, … I_0\)), and one output \(Y\)
A multiplexer can be designed to have m information inputs with \(m < 2^n\) as well as n selection inputs

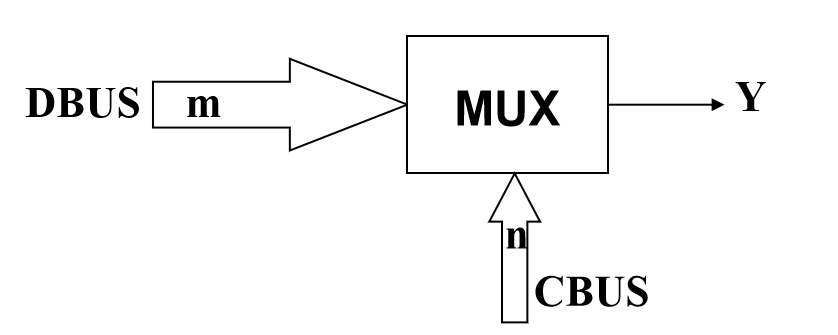
2-to-1-Line Multiplexer¶

The single selection variable S has two values:
- S = 0 selects input \(I_0\)
- S = 1 selects input \(I_1\)
The equation:\(Y =\overline{S}I_0 + SI_1\)
The circuit:

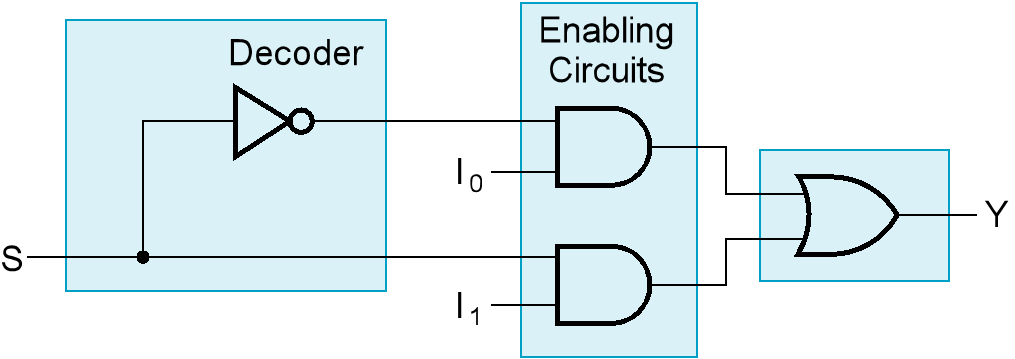
Multiplexer Width Expansion(选择多位)¶

example:4-to-1-line quad multiplexer¶

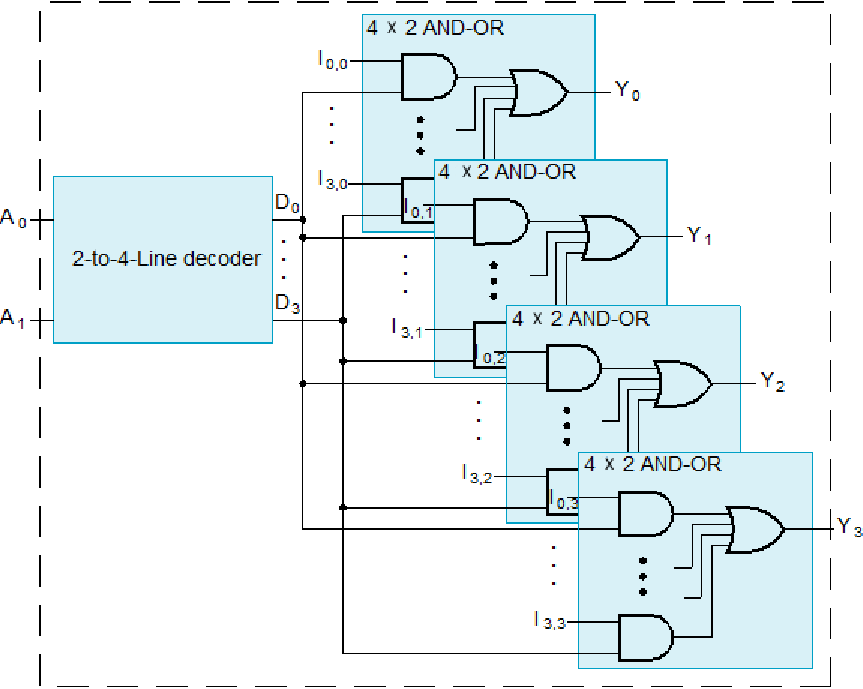
Other Selection Implementations¶

Three-state logic in place of AND-OR。 Gate input cost = 18

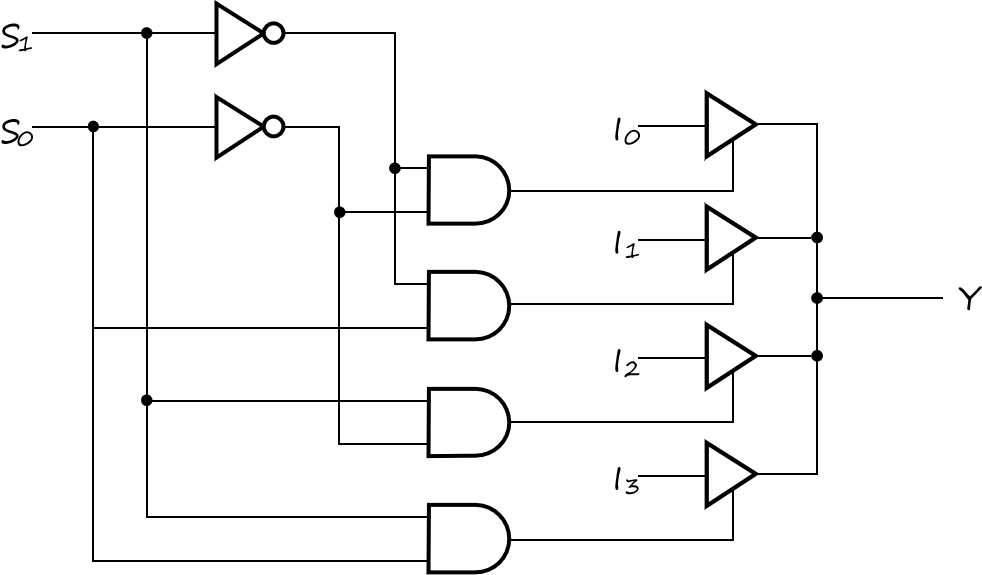
Distributing the decoding across the three-state drivers（分层选择） Gate input cost = 14

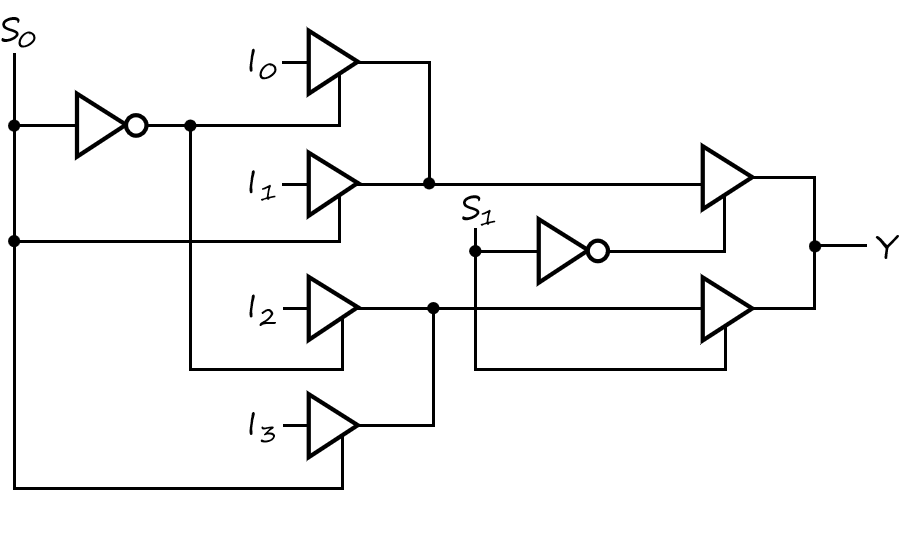
基于传输门的

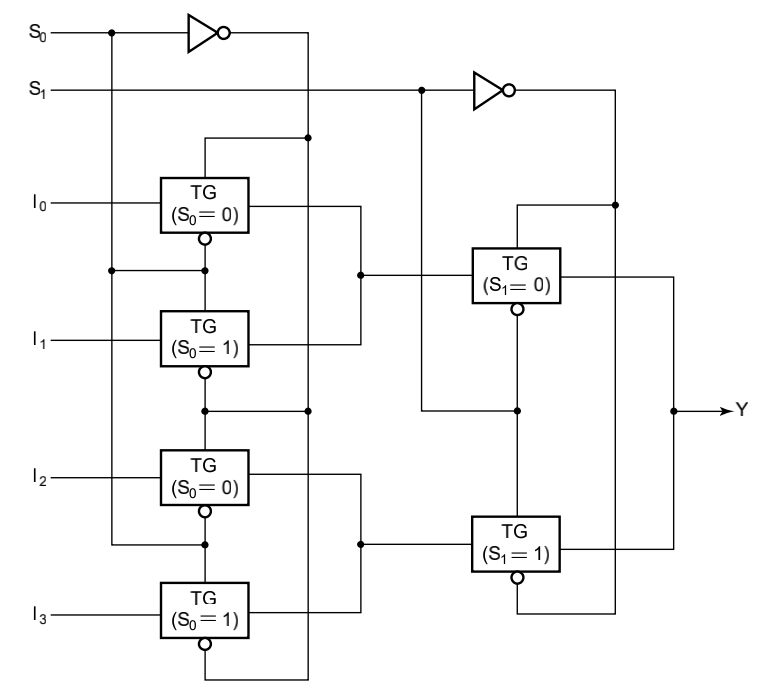
Combinational Logic Implementation- Multiplexer Approach 1¶

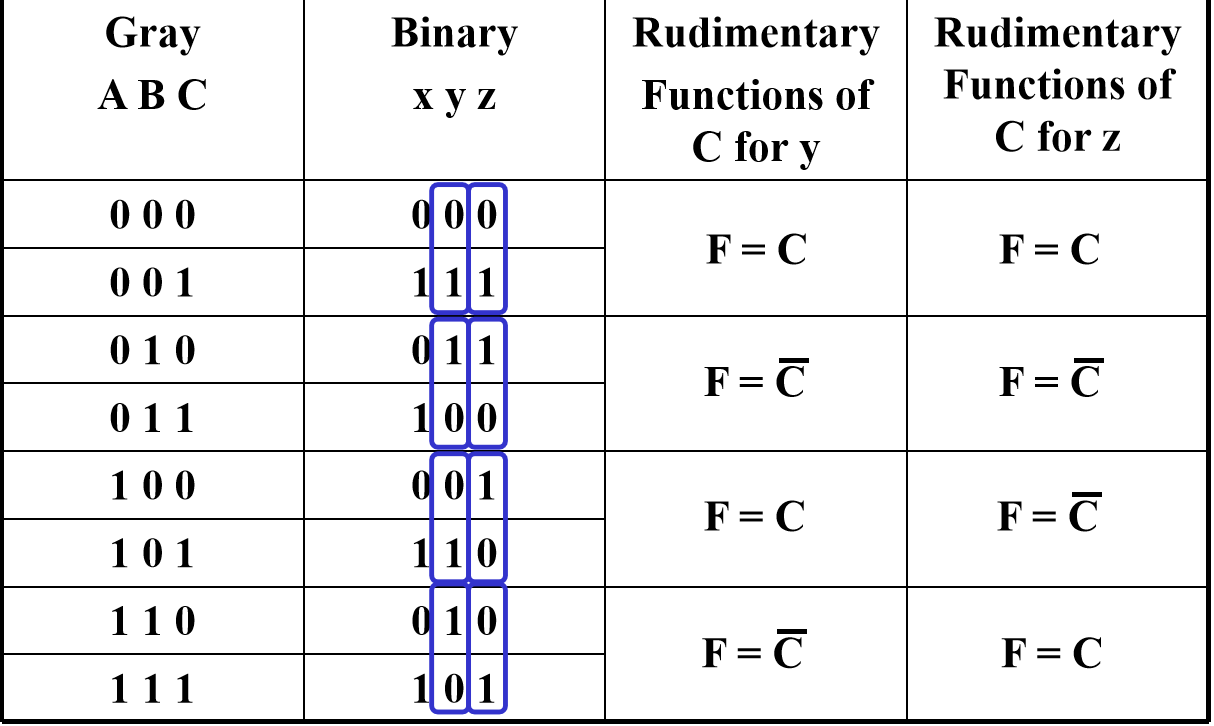
查找表

Combinational Logic Implementation - Multiplexer Approach 2¶

Part 3 Arithmetic functions¶

Function Block¶

Half-Adder¶

两输入两输出

\(S\)为\(X\oplus Y,\)\(C\)为\(XY\)

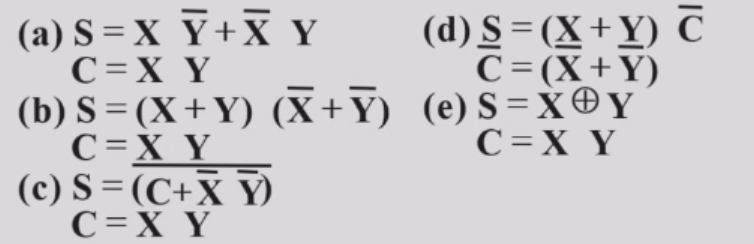
常见两种电路实现

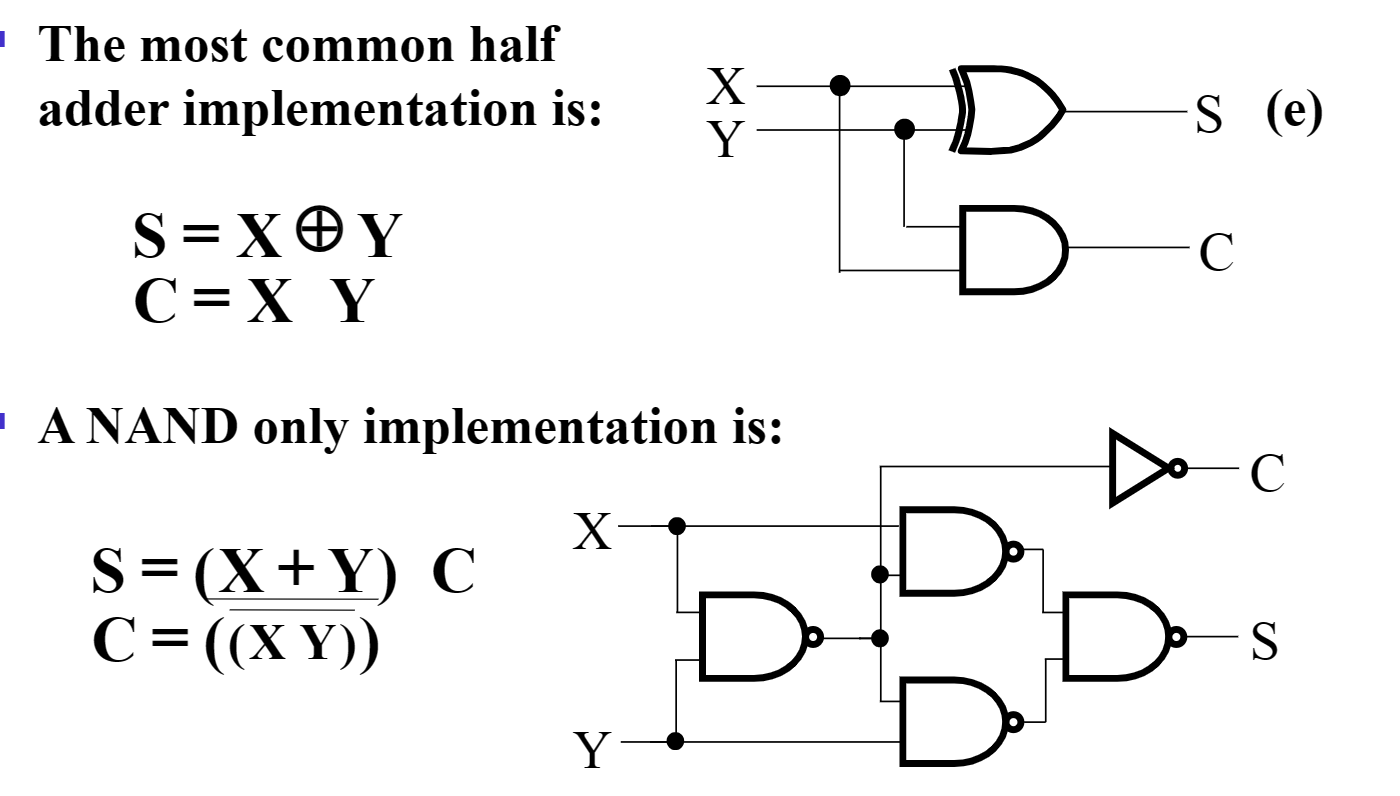
Full-Adder¶

全加器即考虑上一位的进位，即\(Z\)or\(C_i\)

S=\(\overline{C_i}(A\oplus B)+C_i(\overline{A\oplus B})\)

The term \(X\cdot Y\) is carry generate,\(X\oplus Y\) is carry propagate

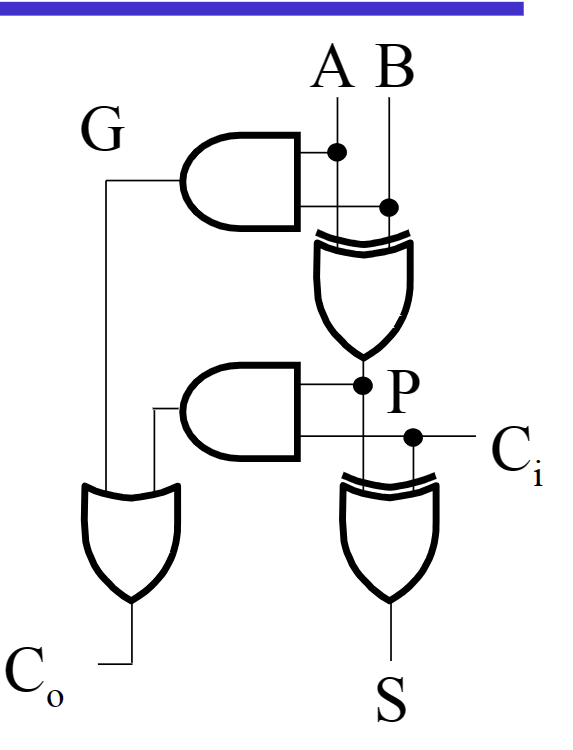
Ripple-Carry Binary Adder:需要延时行波进位加法器

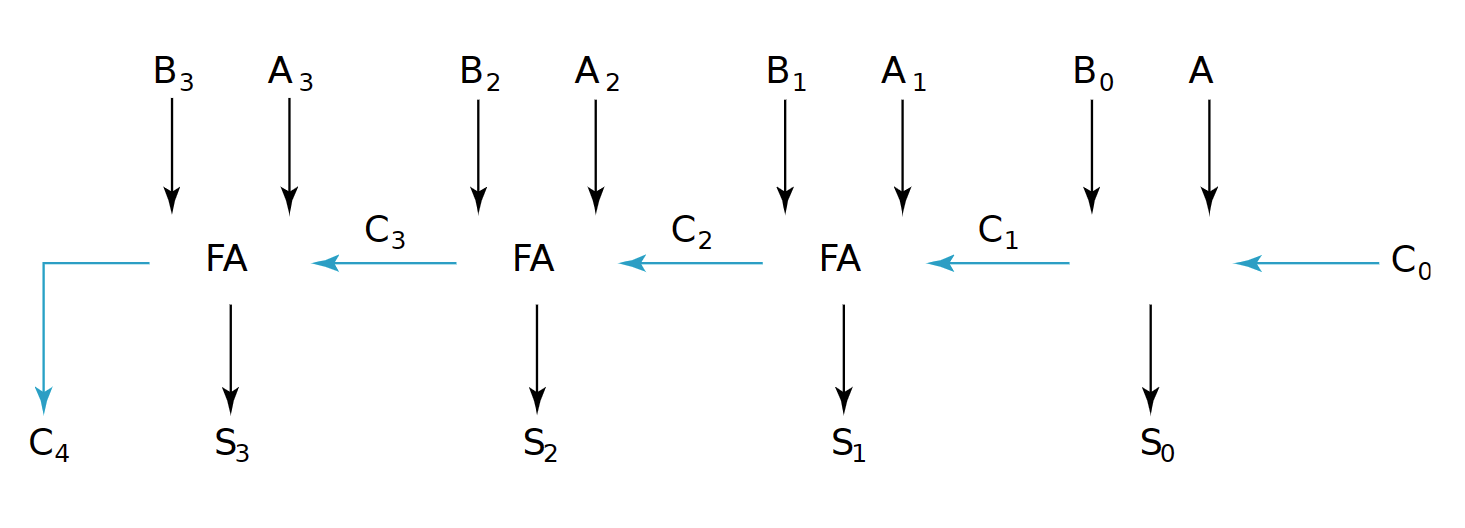
Group Carry Lookahead Logic 超前进位加法器

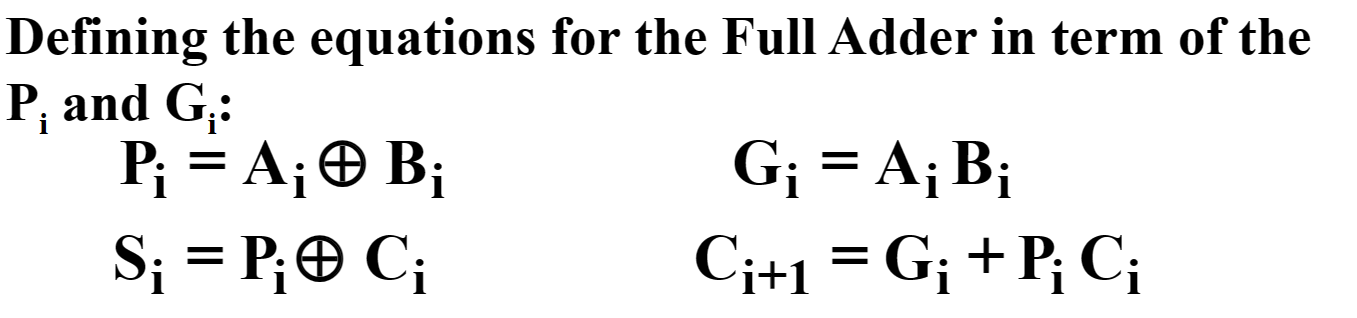
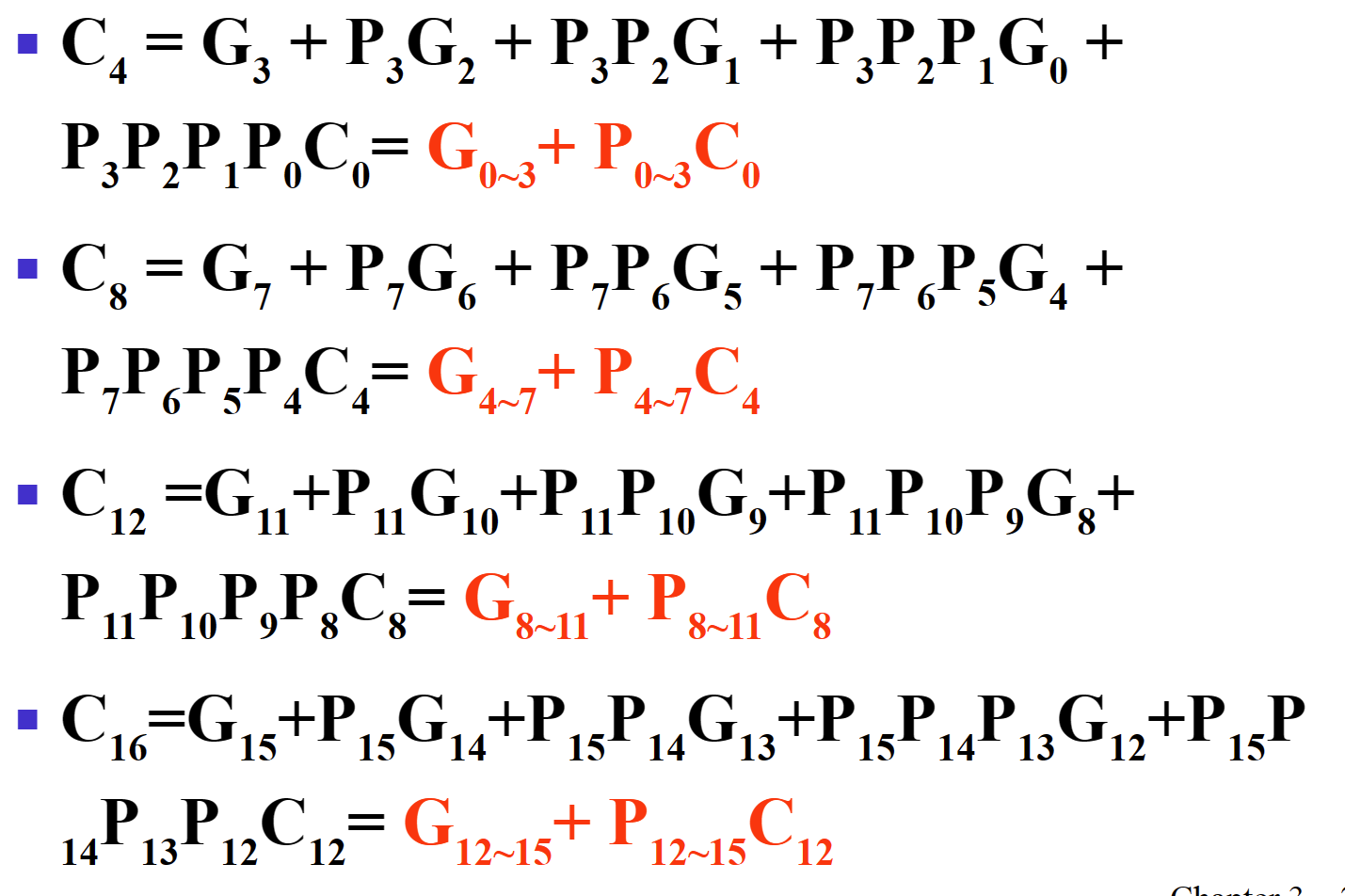
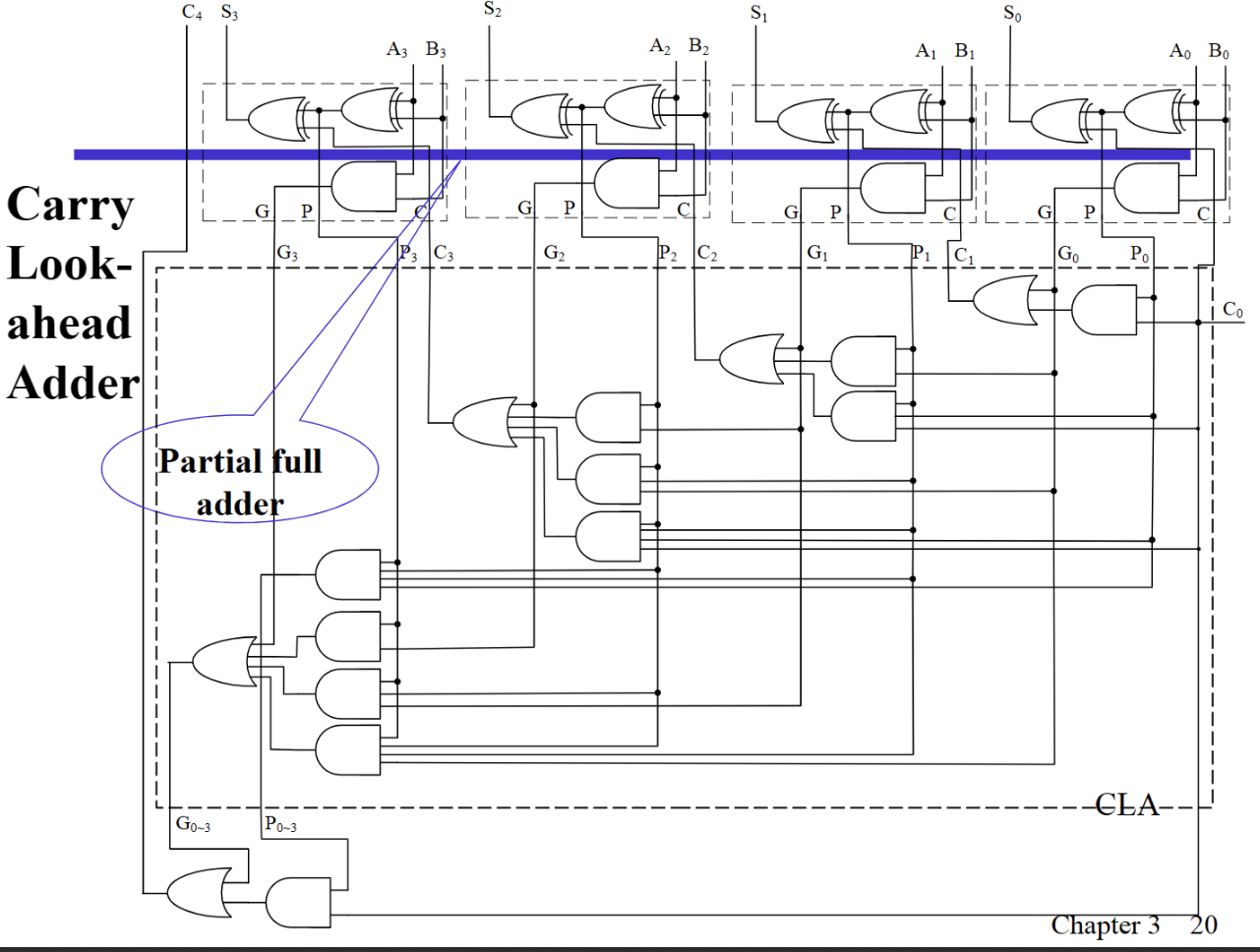
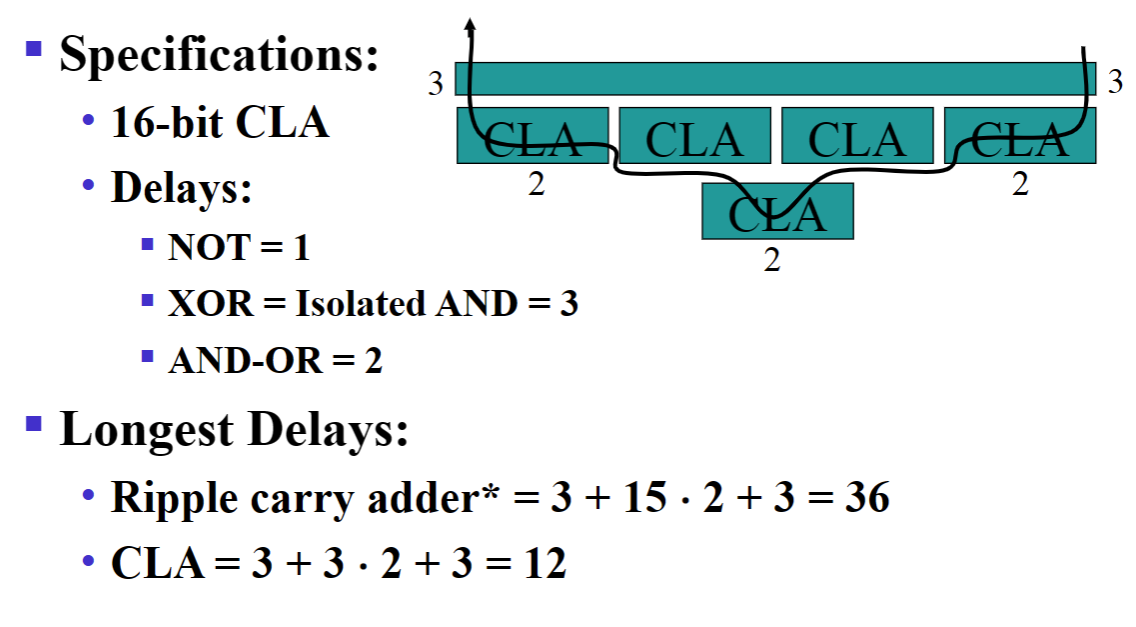
每次使用上一块的进位结果，每一次进位结果延迟为3

Unsigned Subtraction¶

Complements 补码¶

Diminished Radix Complement of N: defined as \((r^n-1)-N\) ,known as 反码 \(1's\) complement
Radix Complement: defined as \(r^n-N\) \(2's\) complement
补码：对n位二进制数，相当于第一位\(a_{n-1}\)代表\(-2^{n-1}\),后续每位都代表\(2^k\)

即M-N时，减数N先求补码\(2^n-N\)，然后\(M+(2^n-N)\),若产生进位1，说明够减，对应值即为答案；若进位为0，说明不够减，则对结果取补码并加负号

有符号减法¶

设加法为0，减法为1，正数第一位0，负数第一位1，那么对减数第一位，符号，被减数第一位构成的序列，若有偶数个0，在没有溢出情况下则可以转化为同号相加
若被加数与被减数为负，则取对应补码（不改变符号位），之后若是加法则正常进行，减法则类似地对减数取补

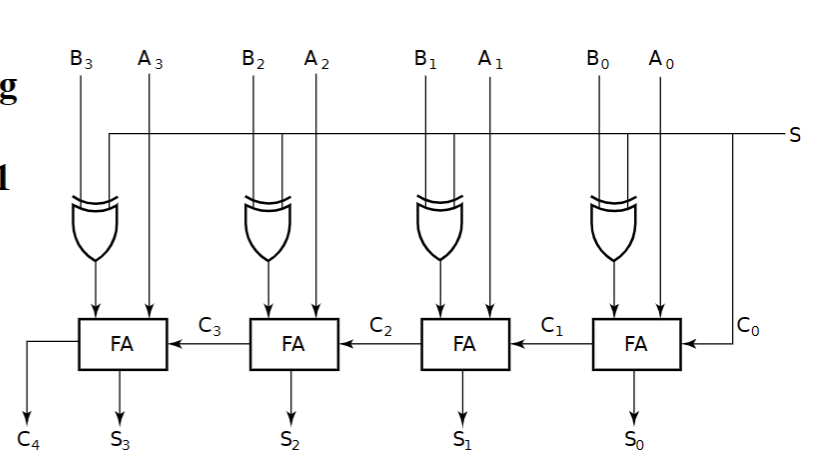
S=1为减法器，S=0为加法器

溢出¶

同号相加、异号相减时可能会出现溢出

判断溢出：\(V=C_n\oplus C_{n-1}\),即\(C_n\)与\(C_{n-1}\)符号一致则不溢出，否则溢出

两个正数相加，\(C_n\)一定是0，溢出只可能是\(C_{n-1}\)为1

两个负数相加，\(C_n\)一定是1，若不溢出\(C_{n-1}\)需要为1

无符号数溢出：两个首位都是1
有符号数：同号时有可能溢出

常数除法、乘法¶

对于2的幂次可以通过移位得到结果，对于非2幂次可以常数加法和2的幂次乘除相结合得到结果。

如\(3x=2^1x+2^0x\),即\(x[31:0]=\{x[30:0],1'b0\}+x[31:0]\).

压缩、递增、递减¶

压缩：针对特定应用时简化已有模块，如递增递减等

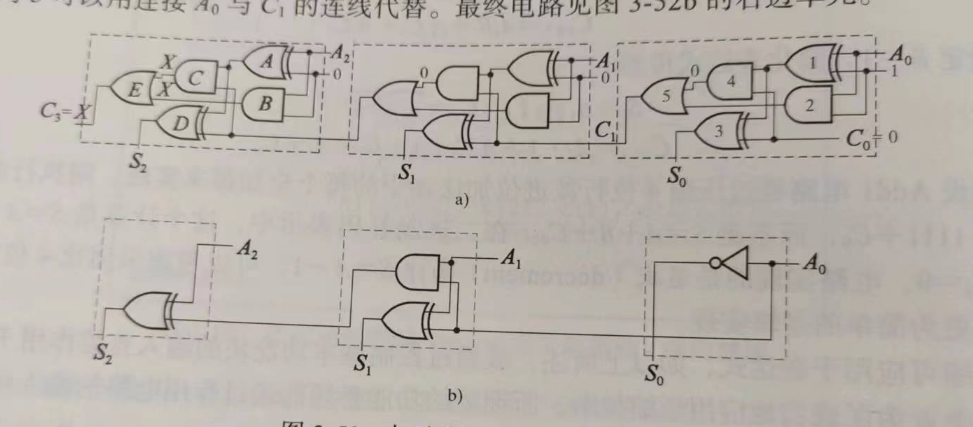
零填充与符号扩展¶

增加输入位数：在高位添加或在低位添加，前者适用于加减，后者适用于低精度乘法