Curves¶
Implict Curves¶
- Advantages: easy to determine if a point is on the curve
- Disadvantage: difficult to find all points on it
- Display
- Subdivision
- 注意仅凭格子四个顶点值相同,也不一定能不继续细分,因为可能在格子中心发生符号变换。
Parametric Curves¶
- variable is a scalar and function is a vector
Interpolation¶
- nearest neighbor interpolation 直接和最近采样点值相同
-
linear interpolation 线性插值,值连续但是导数不连续
-
smooth interpolation
-
cubic hermite interpolation
- given: 两个点的值和导数
- 做一个三次多项式插值 \(P(t)=at^3+bt^2+ct+d\)
- 直接带入求解就行
-
Hermite Basis Functions
\[
P(t)=\sum_{i=0}^3h_iHi(t)
\]
- change basis
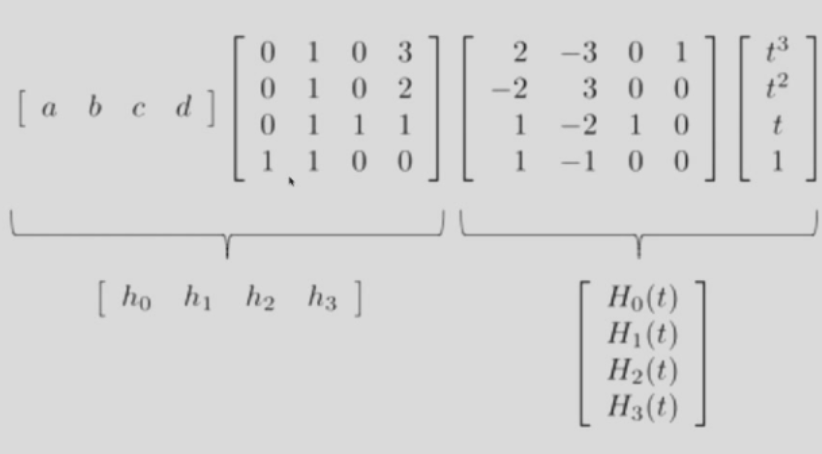
\[
\begin{aligned}
&H_{0}(t) =2t^3-3t^2+1 \\
&H_1(t) =-2t^3+3t^2 \\
&H_2(t) =t^3-2t^2+t \\
&H_3(t) =t^3-t^2
\end{aligned}
\]
- Catmull-Rom interpolation
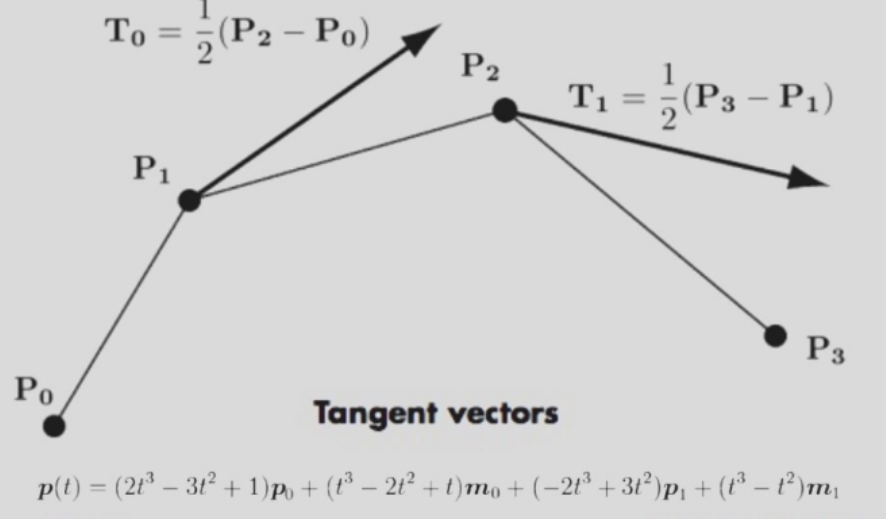
Bezier Curve¶
\[
C(t)=\sum_{i=0}^nP_iB_{i,n}(t),t\in[0,1]
\]
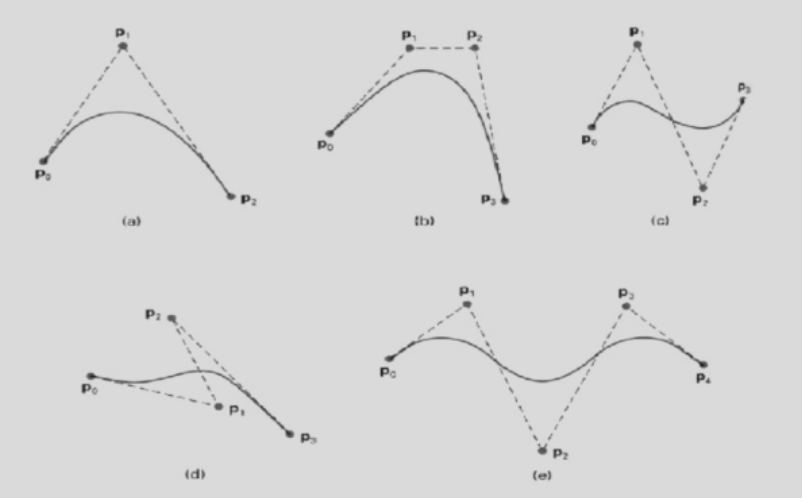
- \(P_o\)是control points 其中曲线穿过始末控制点
- 第一和第二个点连线恰为第一个点处的切线,同理倒数第二个和最后一个点连线恰为最后一个点处的切线
- \(B_{i,n}(t)=C_n^it^i(1-t)^{n-i}\)
- 0到1非负
- \(\sum_{i=0}^nB_{i,n}(t)=1\)
- \(B_{i,n}(t)=B_{n-i,n}(1-t)\)
- \(B_{i,n}(0)=1,i=0;=0,else\)
- \(B_{i,n}(1)=1,i=n;=0,else\)
- 对称性
- affine invariance
- convex hull 贝塞尔曲线被包裹在其控制点连成的凸包中
-
variation diminishing 一条直线穿过凸包,与贝塞尔曲线的交点数不超过与控制多边形的交点数
-
rational Bezier Curve 用户控制权重
\[
R(t)=\frac{\sum_{i=0}^{n}B_{i,n}(t)\omega_{i}P_{i}}{\sum_{i=0}^{n}B_{i,n}(t)\omega_{i}}=\sum_{i=0}^{n}R_{i,n}(t)P_{i}
\]
-
缺点:牵一发而动全身 一个控制点会影响整个curve
-
Non-Uniform Rational B-Splines 用户指定控制点控制范围