2D Graphics

Rasterization

1. Convert 2D primitives (lines, polygons,filled/patterned regions, etc.) into a raster image

   • For output on a monitor/printer
   • Rasterization or Scan Conversion

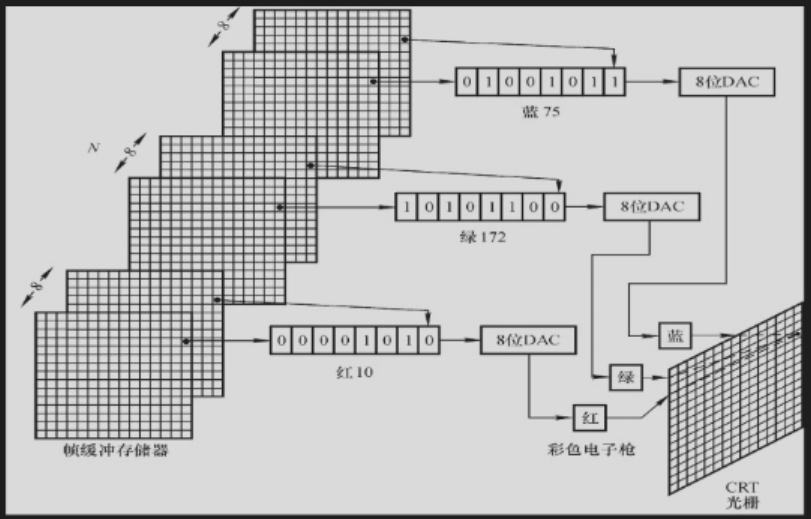
• 液晶：亮度通过偏振片控制，因此显示黑色时会出现漏光问题

1. Raster Graphics Packages

• The efficiency is critical to the performance of a display system
• The raster graphics package is typically a collection of efficient algorithms for scan converting (rasterizing) primitives
• High performance graphics workstations have most of these algorithms implemented in hardware
  • Modern PCs (video cards)

Line Segment

1. Coordinate System

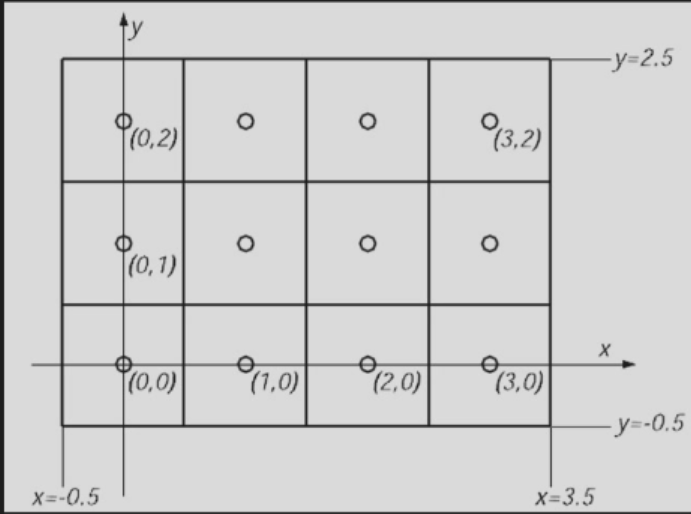
2. The line is a powerful element used since the days of Euclid to model the edges in the world

3. Given a line segment defined by its endpoints, determine the pixels and color which best model the line segment.

4. Requirements

   • the selected pixels should lie as close to the ideal line as possible
   • the sequence of pixels should be as straight as possible
   • all lines should appear to be of constant brightness independent of their length and orientation
   • should start and end accurately
   • should be drawn as rapidly as possible
   • should be possible to draw lines with different width and line styles

5. Equation of a line

   • \(y=mx+c\)
   • 对于线段端点 \(P(x_1,y_1),P(x_2,y_2)\)
   • 可以计算斜率，x每增大单位长度，y增大m

6. Digital Differential Analyzer(DDA)

   • 只考虑first octant
   
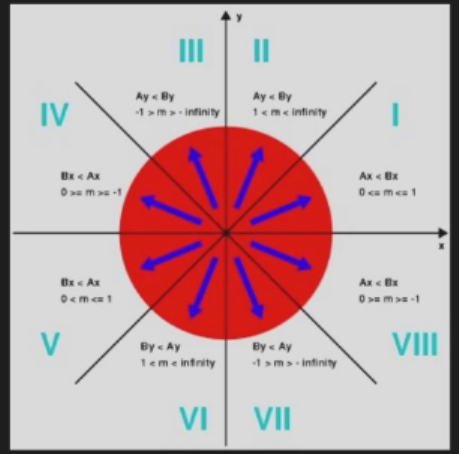
   • use differential equation
   • increment x by 1
   • \(x_i=x_{i,prev}+1,y_i=y_{i,prev}+m\)
   • \([x_i,round(y_i)]\)

7. DDA is an incremental algorithm, uses floating point operations, which are very cleverly avoided in an algorithm.

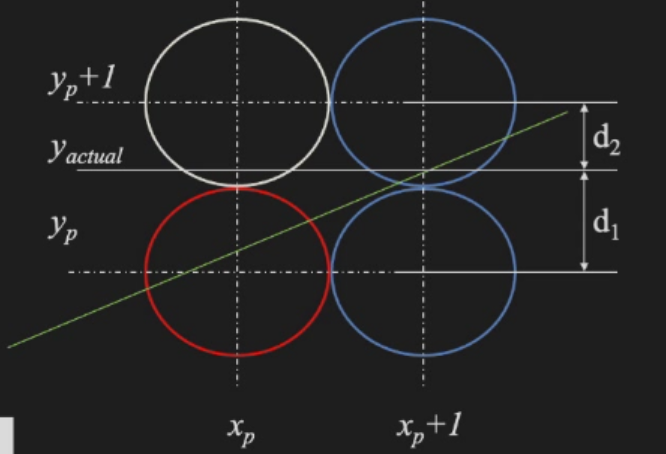
8. Bresenham's Line Drawing

   • 小于45°时，y只有两种选择，不变或加1
   

Circles

1. scan converting a circle

2. Bresenham's Algorithm

• 加速的问题：sin和cos的误差会不断累积

Polygon Filling

1. representation:

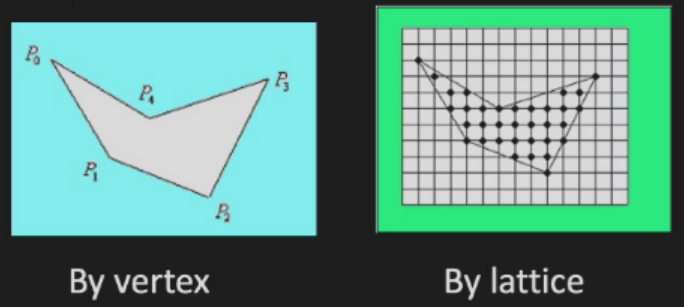
2. filling: vertex representation -> lattice representation

   • fill a polygonal region -> test every pixel in the raster to see if it lies inside the polygon

3. even-odd test: 引一条射线与图形交点奇数个则图形内，偶数个则图形外

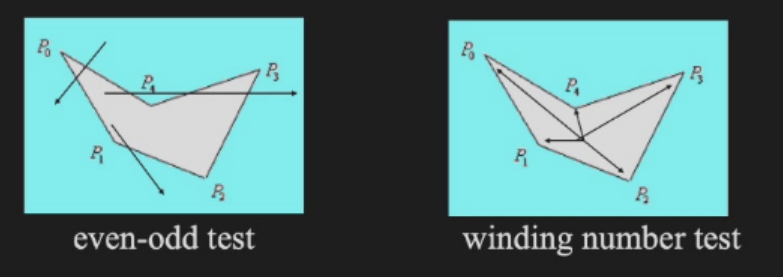
4. winding number: 按顺序遍历所有顶点和此点连线对应向量，根据旋转过的角度判断是否在图形内。或从一点做射线，在此之前首先制定一个多边形环绕方向，由上往下为负，由下往上为正，判断此射线和边交点的方向，为0则在多边形外，否则多边形内

4. Scan-line Method

   • Use intersections between region boundaries and scan lines to identify pixels that are inside the area
   • Exploit the coherence
     • Spatial coherence: Except at the boundary edges, adjacent pixels are likely to have the same characteristics
     • Scan line coherence: Pixels in the adjacent scan lines are likely to have the same characteristics
   • From top to bottom, from left to right
     • the intersections are paired and in-between pixels are set to the specified intensity
   • Algorithm
     • Find the intersections of the scan line with all the edges in the polygon
     • Sort the intersections by increasing X-coordinates
     • Fill the pixels between pair of intersections
   
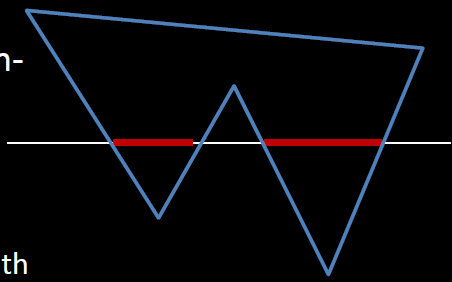
   • Efficiency in Scan-line Method
     • Intersections could be found using edge coherence
     • the X-intersection value \(x_{i+1}\) of the lower scan line can be computed from the X-intersection value \(x_i\) of the preceding scanline as \(x_{i+1}=x_i+1/m\)
     • List of active edges could be maintained to increase efficiency
     • Efficiency could be further improved if polygons are convex, much better if they are only triangles
   • Special cases
   
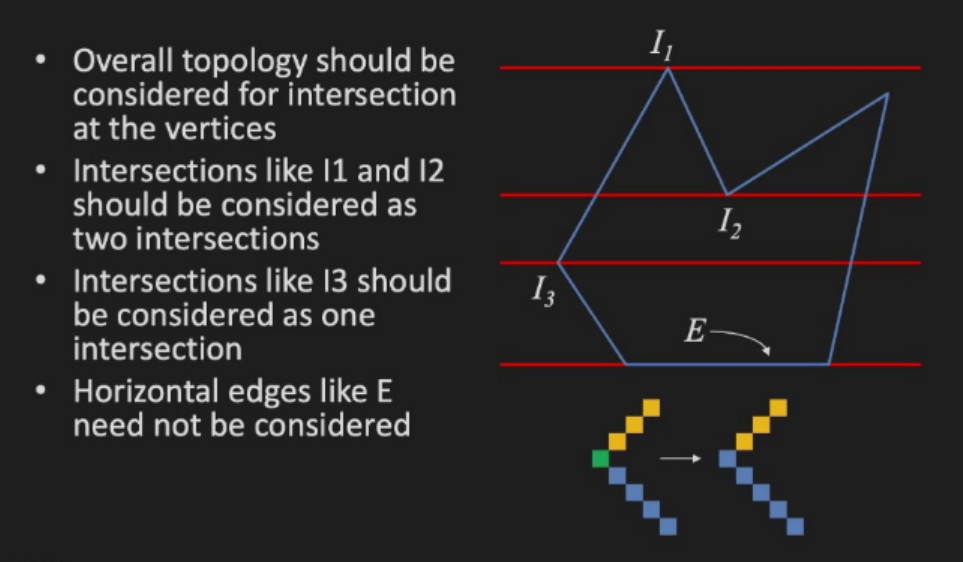
   • Advantages:
     • efficient
     • each pixel is visited only once
     • shading algorithms could be easily integrated to obtain shaded region

5. Seed Fill Algorithm

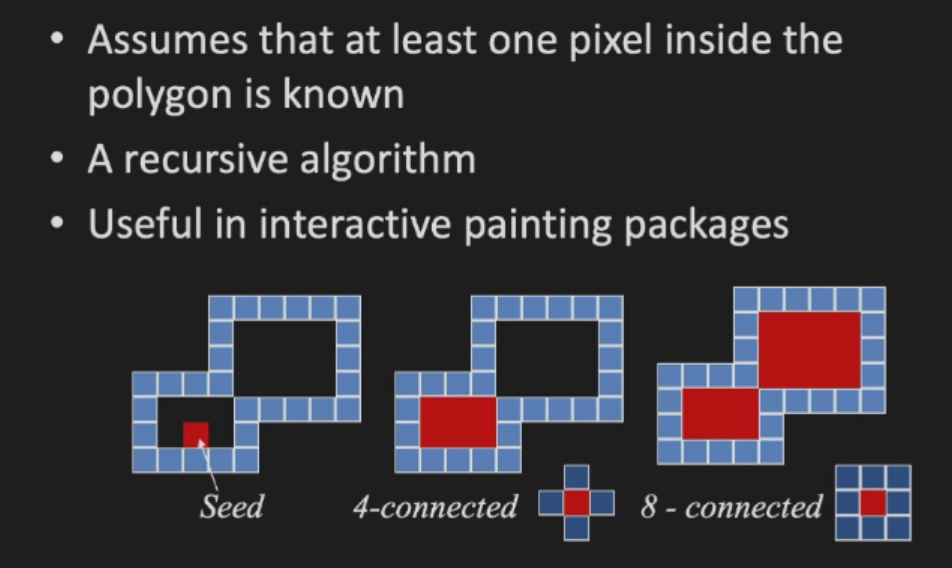
Clipping

1. Clipping: removal of content that is not going to be displayed

   • 屏幕外，camera后，too close or too far
   • usually done before scan converting to make more efficient

评论