Rendering

Monte Carlo Integration

Rendering = Infinite-dimensional Integrals

• 5D Integral: Real Camera Pixel Exposure

• estimate the volume of a d-dimensional sphere

对高维度情况效率会不断下降到0

• Quadrature-based Integration Error $$ Error \sim \frac{1}{n}=\frac{1}{N^{1/d}} $$

• Random Sampling Error 随机采样误差与维度无关 $$ Error=Variance^{½}\sim\frac{1}{\sqrt{N}} $$

• 直至现在为止，蒙特卡洛采样仍然是处理高维导数的唯一办法

1. Overview

   • Idea: estimate integral based on random sampling of a function
   • Strength
     • General and relatively simple
     • Requires only function evaluation at any point
     • Works for very general functions, including discontinuities
     • Efficient for high-dimensional integrals
   • Weakness
     • noisy: 只是平均意义上正确
     • 收敛速度可能很慢，需要大量采样

2. Monte Carlo estimator

   • Define integral \(\int_a^bf(x)dx\)
   • Random variable \(X_i\sim p(x)\)
   • estimator: \(F_N=\dfrac{1}{N}\sum_{i=1}^N\dfrac{f(X_i)}{p(X_i)}\)

3. basic Monte Carlo estimator

   • \(X_i\sim p(x)=\dfrac{1}{b-a}\)
   • so \(F_N=\dfrac{1}{N}\sum_{i=1}^Nf(X_i)\)

4. 蒙特卡洛是unbiased的

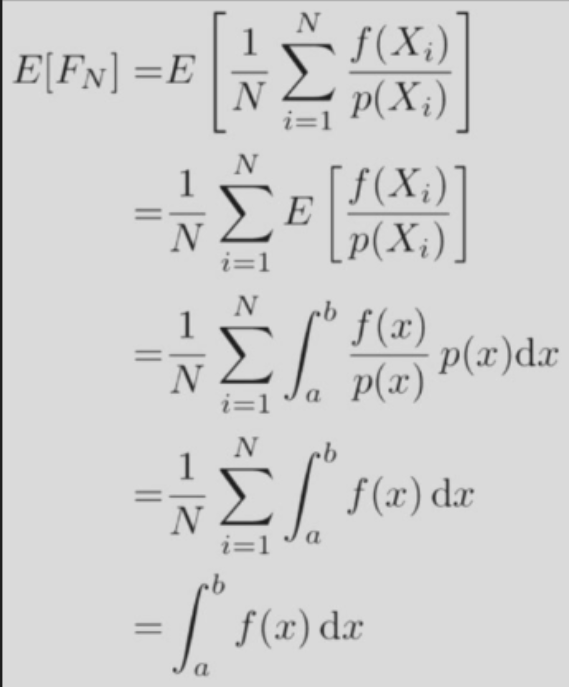
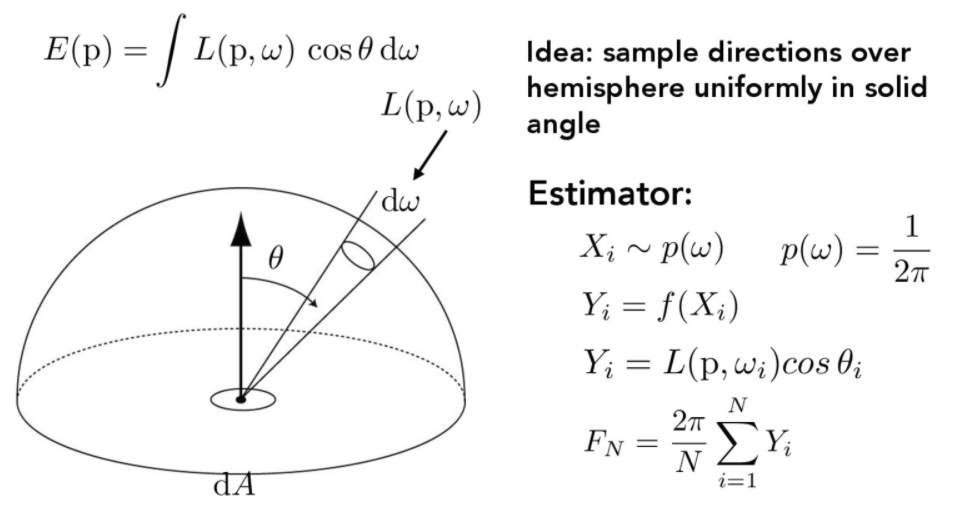
5. Direct Lighting Estimate

   • idea: sample directions over hemisphere uniformly in solid angle

     

6. Importance Sampling 更加高效

   • \(p(x)\)更加接近\(f(x)\)的分布，函数值越大采样概率越高

7. 如果\(p(x)\)精确知道\(f(x)\)，我们只需要一个样本点就够了

Global Illumination

1. deal with infinite dimension: probabilistic termination

   • can design this to be unbiased - this is called Russian Roulette

2. reweight

\[ \left.\left.\left.\mathrm{Let~}X_{\mathrm{rr}}=\left\{\begin{array}{l}\frac{X}{p_{\mathrm{rr}}},\text{ with probability }p_{\mathrm{rr}}\\0,\mathrm{~otherwise}\end{array}\right.\right.\right.\right. \]

unbiased

\[ E[X_{\mathrm{rr}}]=p_{\mathrm{rr}}E\left[\frac{X}{p_{\mathrm{rr}}}\right]+\left(1-p_{\mathrm{rr}}\right)E[0]=E[X] \]

但是会扩大variance

评论