Digital Material Appearence

Introduction

• Light / material interactions
• Absorption
• Reflection: Color, Glossiness
• Transmission
• Transparency

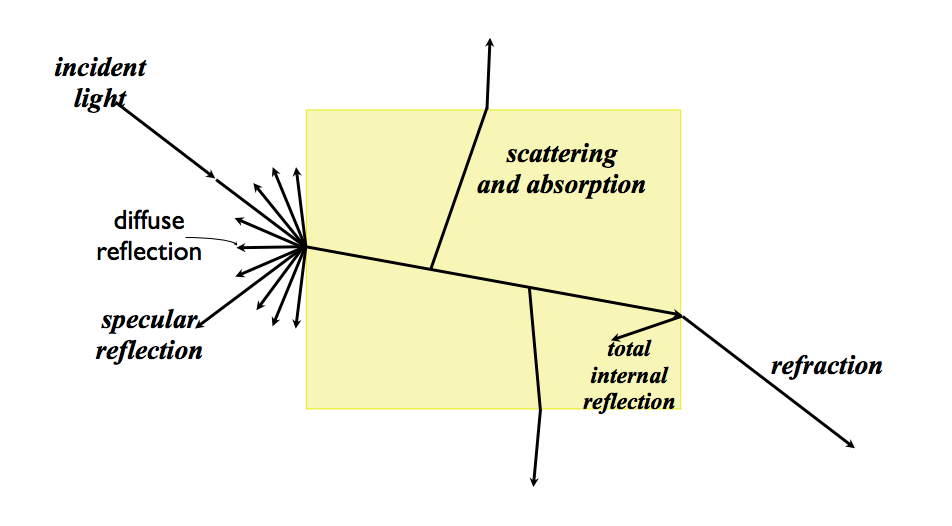
• 和location, view, lighting有关

Reflection Models

介质密度的变化

• BRDF(Bidirectional Reflectance Distribution Function) \(f(i,o)\)，一个四维函数
• 我们知道所有经过同一点的模长为1的向量的集合是一个三维球，在球上表示一个点我们只需要两个参数，因此入射和出射各两个参数，一共四维
• Fixing i, a 2D function of outgoing directions
• describes how incident light is reflected along different directions

Specular Reflection

1. Perfect Mirror Reflection.

   • p: point of interest

   • n: normal

   • i: lighting vector, couting-intuitive dir 方向和实际入射方向相反

   • o: view vector

   • i,o,n are unit vectors

     

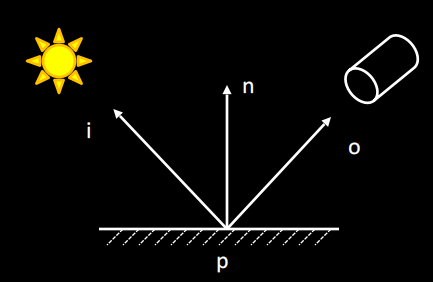
   • 计算反射方向r

     • \(– r = -(i - <i,n>n) + <i,n>n = 2<i,n>n - i\)

     • test if \(<o,r>=1\)

     • 利用half vector \(h=\dfrac{i+o}{\|i+o\|}\) 判断h和n是否重合即可

     

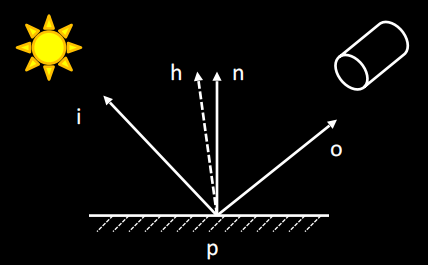
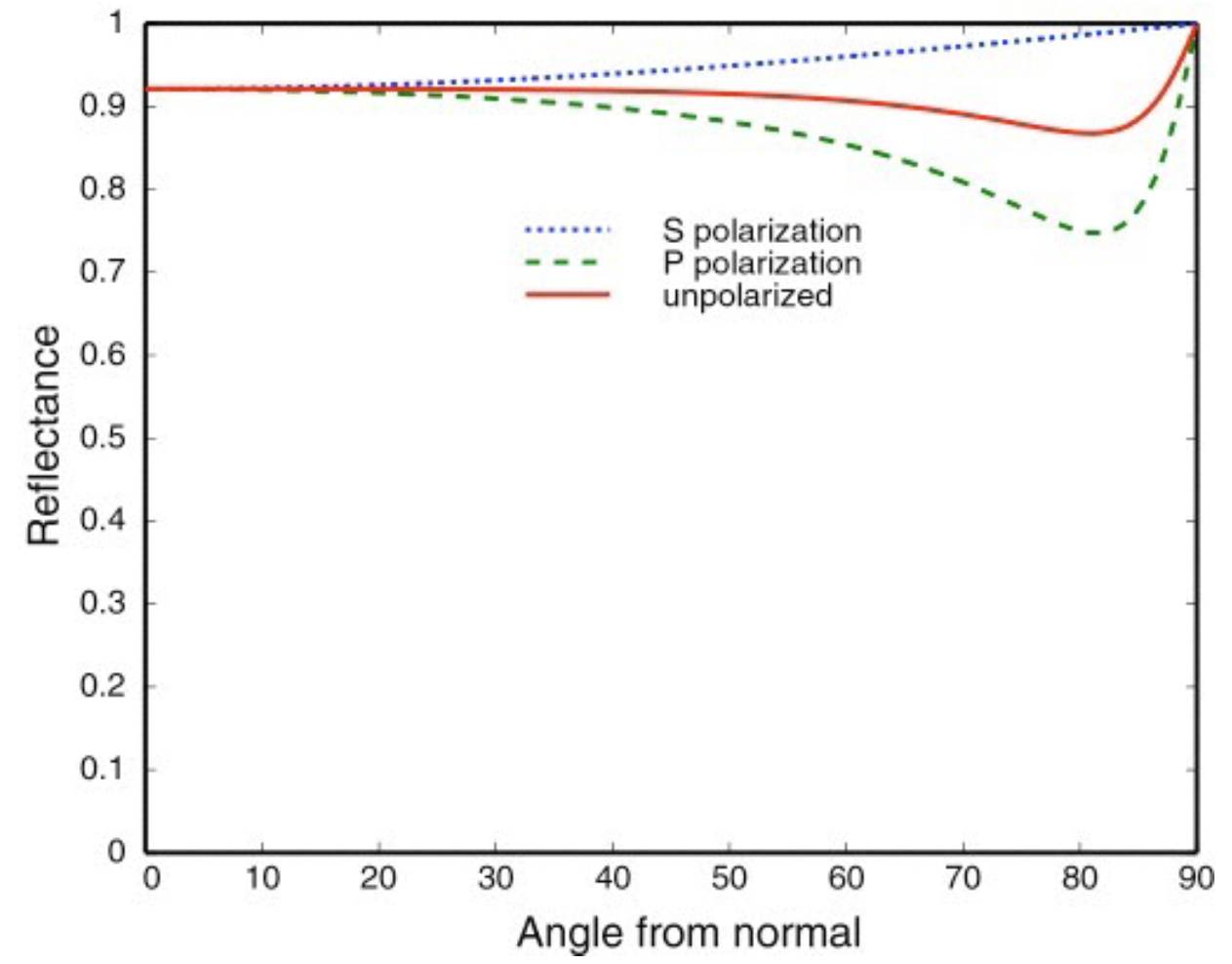
2. Fresnel Reflectance Term: Reflection depends on incident angle

   • 绝缘体

     

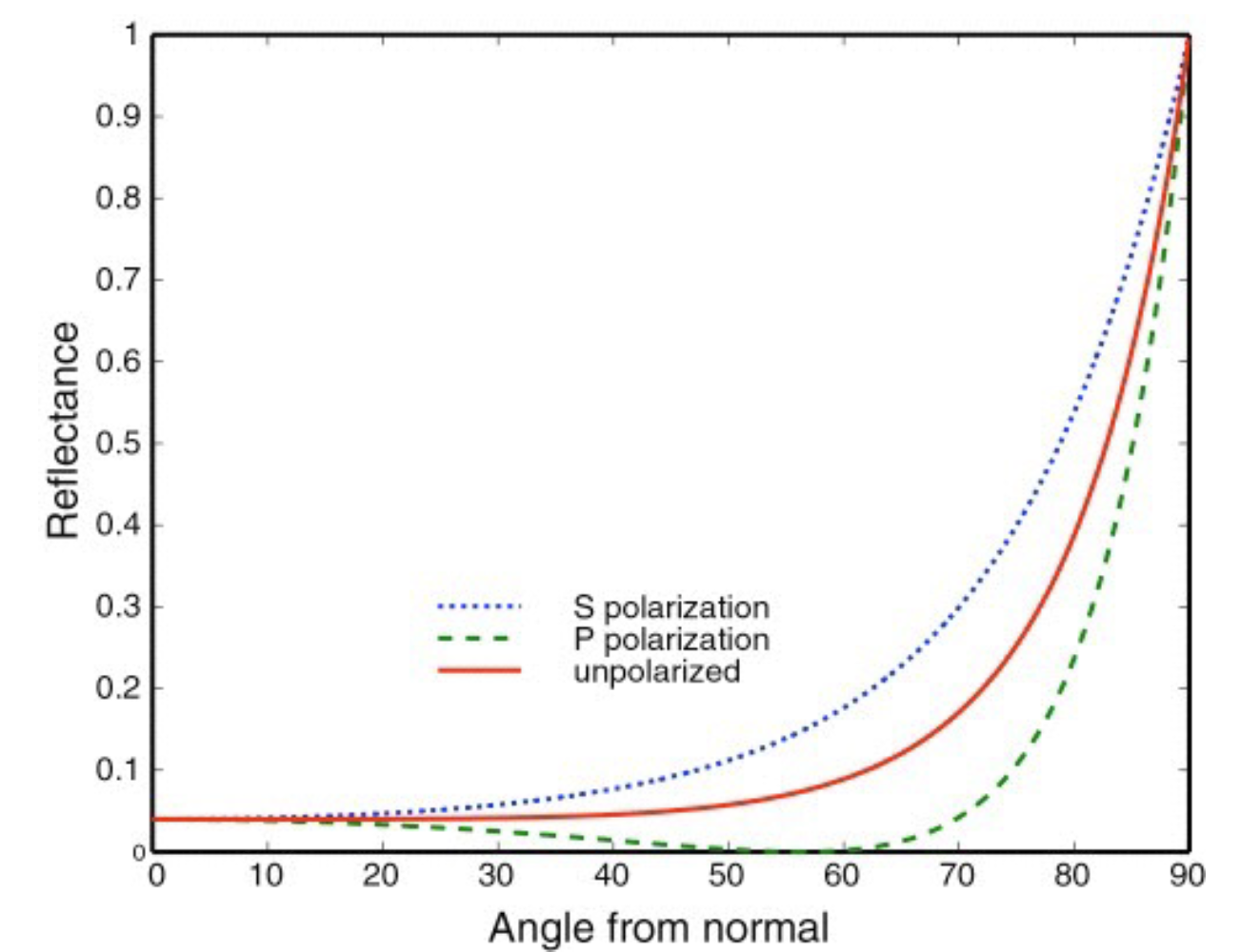
   • 导体

     

   • 公式如下，但显然过于复杂了 $$ R_{s}=\left|\frac{n_{1}cos\theta_{i}-n_{2}cos\theta_{i}}{n_{1}cos\theta_{i}+n_{2}cos\theta_{i}}\right|^{2}=\left|\frac{n_{1}cos\theta_{i}-n_{2}\sqrt{1-\left(\frac{n_{1}}{n_{2}}sin\theta_{i}\right)^{2}}}{n_{1}cos\theta_{i}+n_{2}\sqrt{1-\left(\frac{n_{1}}{n_{2}}sin\theta_{i}\right)^{2}}}\right|^{2} $$

     \[ R_{p}=\left|\frac{n_{1}cos\theta_{i}-n_{2}cos\theta_{i}}{n_{1}cos\theta_{i}+n_{2}cos\theta_{i}}\right|^{2}=\left|\frac{n_{1}\sqrt{1-\left(\frac{n_{1}}{n_{2}}sin\theta_{i}\right)^{2}-n_{2}cos\theta_{i}}}{n_{1}\sqrt{1-\left(\frac{n_{1}}{n_{2}}sin\theta_{i}\right)^{2}+n_{2}cos\theta_{i}}}\right|^{2} \]

3. 采用Schilick’s Approximation,其中\(\theta\)是i和n的夹角

\[ \begin{aligned} &R(\theta)=R_0+\bigl(1-R_0\bigr)(1-cos\theta)^5 \\ &R_0=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2 \end{aligned} \]

4. Microfacet-Based Models: Many real-world materials actually consist of or can be modeled as microfacets

   • Microfacets = Tiny, planar and mirror-like surface patches
   • Key: the distribution of microfacets’ normals 不同的法向量会影响反射的结果

   $$ f(i,o)=\frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)} $$

   F:反射率 D:微面法向量的分布

   D(h) describes the percentage of microfacets whose n = h (i.e. the normal distribution of microfacets)

   • Microfacets that could potentially reflect under the current i & o 必要条件而非充分

   G表示Shadowing & Masking 光打不到或者反射光被物体遮挡

   • Microfacets in shadows do not reflect
   • Microfacets occluded cannot be seen
   

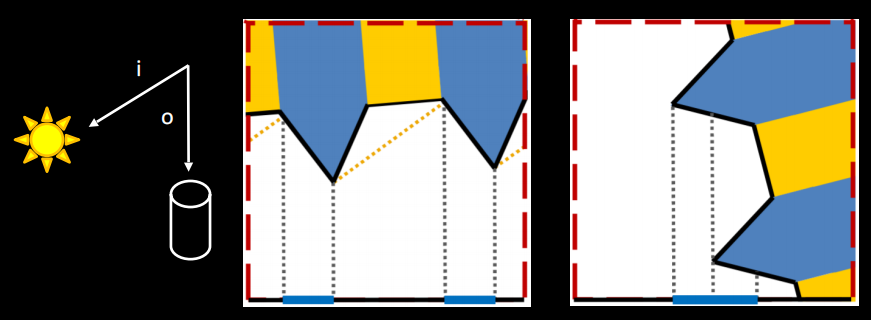
   Different microfacet BRDFs mainly differ with the choice of D

5. An Example: Cook-Torrance Model。D为Beckman distribution。m控制highlight的形状 $$ D=\frac{e^{\frac{-(an^2(a)}{m^2}}}{\pi m^2cos^4(\alpha)}, \alpha=\arccos(\mathrm{n}\bullet h)\G=\min(1,\frac{2(h\bullet n)(o\bullet n)}{o\bullet h},\frac{2(h\bullet n)(i\bullet n)}{o\bullet h}) $$

6. 以上我们都是isotropic的，即各向同性的，所以高光会是圆形的。如果需要条形的，这时候就要anisotropic(各向异性) BRDF

7. Diffuse Reflection

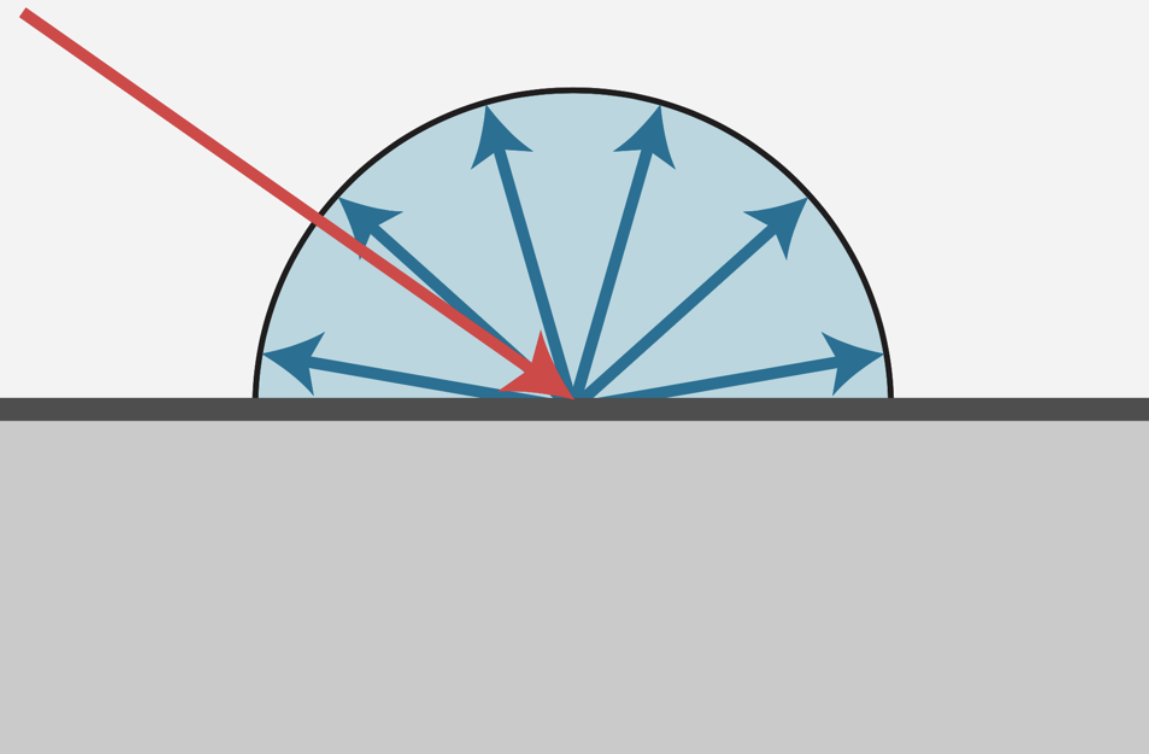
   • Lambertian model

   • Light is equally reflected along all outgoing directions

   • Can be considered as highly spread-out random microfacets

   • f(i,o) = constant

     

8. Putting Things Altogether

   • The reflected light of a unit amount of directional incident light can computed as
     $$ f(i,o)(i,n)=\left\frac{\rho_d}\pi+\rho_s\bullet f_{spec}(i,o)\right $$

   • \(\rho_d,\rho_s\) are diffuse/specular coefficients 三个分量，RGB，各算一遍

     • 非导体\(\rho_s\)一般是白色，导体的一般是其本身颜色

   • Could be extended to represent reflectance at different wavelengths

9. 高质量的数据：[Matusik et al. 2004] 每一个BRDF大概都要占64MB，高质量的

10. useful tool
    • Disney’s BRDF Explorer

Reflectance Capture

采集BRDF

1. motivation: Accurate modeling of real-world materials

2. direct sampling: General Idea

   • For each o, For each i, Measure f(i,o)
   • The most general approach / highest quality
   • Extremely time consuming: Curse of dimensionality

3. Illumination Multiplexing

   • Light Stage
     • Use hundreds of light sources simultaneously
     • Only one or a couple of cameras
     • Project certain patterns and recover the reflectance with a lookup table
     • Far more efficient
   • 在电影行业广泛应用
   

评论