ADS Brief Review¶

1 AVL Tree, Splay Tree¶

AVL 插入删除的时间复杂度都是\(O(\log n)\)
\(n_h=F_{n+2}-1\)
Splay: 把所有结点的后代取对数然后求和的方式定义势函数 \(\sum\limits_{i\in T}\log S(i)\)

则均摊代价\(\sum\hat{c_i}\leq1+3(R_2(x)-R_1(x))\)

Splay 搜索插入删除都是\(O(\log n)\)

2 Red-Black Tree and B+ Tree¶

Red-Black¶

n 个内部结点的红黑树高度至多\(2\log(n+1)\)
以 X 为子节点的子树至少有\(2^{bh(x)}-1\)个内部结点
插入：\(O(\log n)\),其中至多旋转 2 次，染色 \(O(\log n)\)
删除也是\(O(\log n)\),其中至多旋转 3 次，染色 \(O(\log n)\)

B+¶

搜索\(O(\log n)\),插入删除\(O(\frac{M}{\log M}\log N)\)

3 Inverted File Index¶

data retrieval: response time, index space
information retrieval: relevant

4 Leftist Heap and Skew Heap¶

Leftist Heap¶

\(Npl(null)=-1\)
merge 时间复杂度\(O(\log n)\)

\(O(\log N_1+\log N_2)=O(\log N_1N_2)=O(\log \sqrt{N_1N_2})=O(\log(N_1+N_2))\)

Skew Heap¶

base case: 处理 H 与 null 连接的情况时,左式堆直接返回 H 即可，但斜堆必须看 H 的右路径，我们要求 H 右路径上除了最大结点之外都必须交换其左右孩子。
heavy: 如果 P 的右子树结点个数至少是 P 的所有后代的一半（后代包括 P 自身）
\(\hat{c_i}\leq2(l_1+l_2)\) merge 摊还时间复杂度\(O(\log n)\)

5 Binomial Queue¶

\(B_k\)在深度 d 处节点数为\(C_k^d\)
FirstChild, NextSibling 同一层高度由左往右递减，使得 merge 进来的树可以直接放在最左侧
\(!!T\)表示将非零的变成 1

struct BinNode
{
    ElementType     Element;
    Position        LeftChild;
    Position        NextSibling;
} ;
struct Collection
{
    int         CurrentSize;  /* total number of nodes */
    BinTree TheTrees[ MaxTrees ];
} ;

摊还：

插入时一次 cost 为 c 的操作造成森林多了 2-c 棵树，因为 1 次操作把\(B_0\)添加到当前森林，多一棵；其余 c-1 次操作都在 merge，每次减少一棵树
势函数：\(\phi_i\)为第 i 次操作后树棵数

斐波那契堆势函数:\(t(H)+2m(H)\)
conclusion:

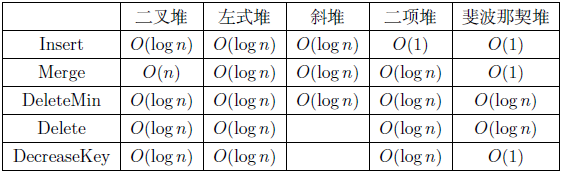
6 Backtracking¶

Turnpike Reconstruction Problem:使用 AVL 树，一次操作\(O(n\log n)\)

7 Divide and Conquer¶

\(T(n)=2T(\lfloor\sqrt(n)\rfloor)+\log n\),令\(m=\log n\)
\(T(n)=T(\lfloor n/2\rfloor)+T(\lceil n/2\rceil)+1\),猜测\(T(n)=O(n)\)，设\(T(n)\leq cn\)但归纳失败，但设\(T(n)\leq cn-d\)归纳成立，有时候减去一个项会有用

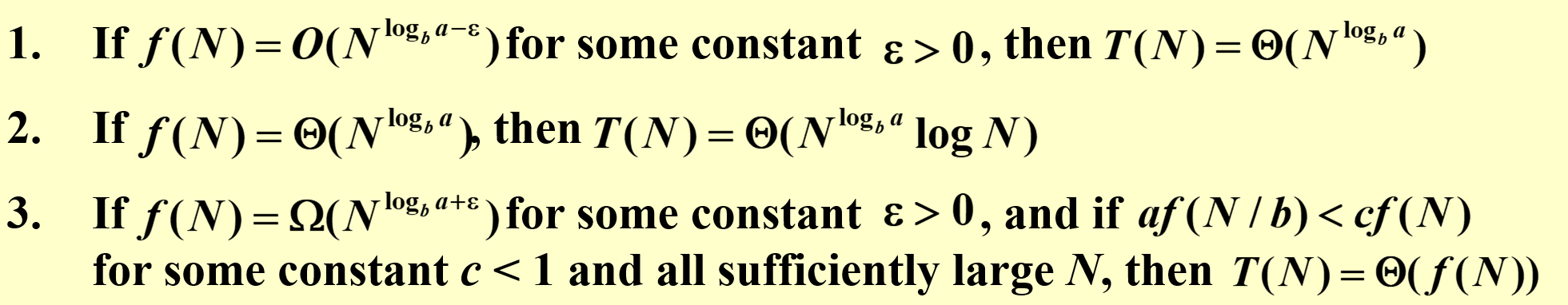
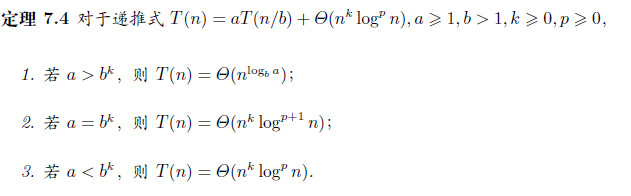
分治法处理逆序对计数时，类似逆序对分成三类，全在左半边，全在右半边，跨越中点。但跨越中点的逆序对个数似乎最多有\(n^2/4\)个，这样分治就失去了时间优势。因此我们基于归并排序，每次计算逆序后也对序列进行排序，因为这并不会影响跨越中点的逆序对。之后在合并过程我们很容易基于 RANK 就可以求出逆序对数目
整数乘法改进，\(ab=10^n a_1b_1+10^{n/2}(a_1b_2+a_2b_1)+a_2b_2\),同时注意到\(a_1b_2+a_2b_1=(a_1+a_2)(b_1+b_2)-a_1b_1-a_2b_2\)，因此我们只需要计算\((a_1+a_2)(b_1+b_2),a_1b_1,a_2b_2\)这三个，因此递推式为\(T(n)=3T(n/2)+O(n)\)，复杂度变成了\(O(n^{\log_23})\)
矩阵乘法，使用分块矩阵

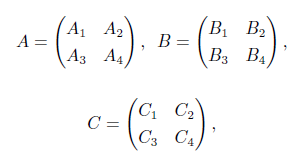
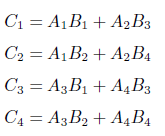
但此时需要计算八个 n/2 规模的矩阵，复杂度仍然是\(O(n^3)\)，但 Strassen 给出了一个天才的构造

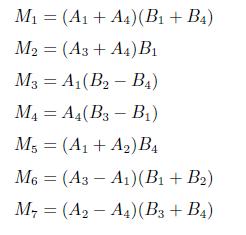
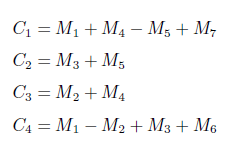
因此\(T(n)=7T(n/2)+O(n^2)\),复杂度为\(O(n^{\log_27})\)

8 Dynamic Programming¶

All-Pairs Shortest Path: \(D^k[i][j]=\min\{length\ of\ path\ i\rightarrow\{l\leq k\}\rightarrow j\}\) - 表示用前 k 个节点从 i 走到 j

9 Greedy Algorithms¶

调度问题：计算任务 i 的\(w_i/l_i\)，从大到小降序调度任务
变体：最小化最大延时，直接按 ddl 从小到大排序
Huffman 每次贪心取两个频率最低的符合最优子结构，证明使用反证，若 k-1 规模的\(T'\)是最优解，那加上(x,y)后 k 规模的\(T\)也是最优解，否则存在\(T^*\)，但此时\(T^*\)删去(x,y)会比\(T'\)cost 更小，矛盾，因此最优。

10 NP-Completeness¶

图灵机的构型\(c=t_mt_{m-1}…t_2t_1\underline{q_i}s_1s_2…s_k\),\(s_i\)和\(t_i\)分别是一直到最右侧和最左侧的非空格子上的内容，当然，如果没有则可以写个 □，图灵计算就指图灵机的一列构型\(c_0,c_1,\cdots,c_n\)
一些概念

P 类问题：确定性图灵机可以在多项式时间内求解
NP 类问题：非确定性图灵机可以在多项式时间内求解
显然\(P\subset NP\)

补类：\(co-C\)为\(C\)的补类，\(co-C=\{L|\overline{L}\in C\}\)

P=co-P 直接把问题的是变成否即可，对于确定性图灵机而言是这样的
若 P=NP，则 NP=co-NP

Karp 归约：\(x\in A\Leftrightarrow f(x)\in B\)，记作\(A\leq_pB\)，则 B 比 A 难
若复杂类 C 中任意问题都能多项式规约到 P，则称 P 是 C-hard 的，若同时 P 也在 C 中，则 P 是 C-complete 的
证明 P=NP，即首先找到一个 NP-complete 的问题，再证明这个问题是 P 的
SAT 问题是 NP-complete 的，\(SAT\leq_p3-SAT\),3-SAT 也是 NP-complete 的
哈密顿回路，旅行商问题(TSP)，clique problem，Vertex cover problem 是 NP-complete 的

给定若干个物品，判断是否可由两个箱子装下是 NP-complete 的

dominating set 是 NP-complete 的

最大割，halting 是 NP-hard 的

\(clique\leq_pvertex\ cover\)
Clique problem: Given an undirected graph G = (V, E) and an integer K, does G contain a complete subgraph (clique) of (at least) K vertices?
Vertex Cover: 存在顶点的一个子集，每一条边都有一个顶点在其中
dominating set:给定一个图 G=(V,E)和一个整数 k，我们需要判断是否存在一个大小为 k 的集合\(S\subset V\)，使得每个点要么在 S 中，要么与 S 中的某个点相邻。

11 Approximation¶

最小工时调度问题，m 台机器，不排序基础上近似比为\(2-\dfrac{1}{m}\)，先排序后调用算法则有\(\dfrac{4}{3}-\dfrac{1}{3m}\)
装箱

Next Fit(NF):近似比 2
Any Fit(AF):
- First Fit(FF): 选择最早打开的箱子优先填入
- Best Fit(BF): 选择最满的
- Worse Fit(WF): 选择最空的
以上都是在线的，在线算法的最理想近似比是\(\dfrac{5}{3}\)
Almost Any Fit(AAF): 那么除非当前物品无法装进前 k-1 个箱子里，否则它不会装进第 k 个箱子里
- FF 和 BF 都是
- 为了使 WF 是，我们对它进行如下修正，修正后的为 AWF(Almost Worst Fit) 将当前物品放入能装下它的剩余空间第二大的箱子中；若这样的箱子不存在，便将其放入能装它的剩余空间最大的箱子中，它属于 AAF
- AAF 的近似比都是 1.7
离线算法：允许先排序后再调用对应算法
- First Fit Decreasing(FFD)
- 绝对近似比\(FFD(I)\leq\dfrac{3}{2}OPT(I)\)
- 渐近近似比\(FFD(I)\leq\dfrac{11}{9}OPT(I)+\dfrac{6}{9}\)

k-中心问题：要求选择 k 个中心，使得每个点到最近的中心的距离最大值 r(C)最小化

在给定最优解是情况下有 2-近似算法
- solution 1:每次随机从剩余中取一个，并删去所有距离小于等于 2r 的，r 为最优解
- solution 2:每次取离当前 center 集合最远的点 smarter
除非 P=NP，否则 K-center 问题不存在 ρ-近似算法(ρ<2)

The Knapsack Problem — 0-1 version 近似比为 2
vertex cover 的贪心算法：任意一条边(u,v)，然后将 u 和 v 同时加入到 C 中，然后把 u 和 v 所在的所有边全部移除，是 2-近似算法

12 Local Search¶

Hopfield 神经网络

\(w_es_us_v<0\)的边为好的，否则为坏的
\(\sum\limits_{v:e=(u,v)\in E}w_es_us_v\leq0\)为满意的顶点，否则不满意
state_flipping 每次翻转一个不满意的点，好边权重和都上升，但这有上限，因此必然停止
最多经历\(\sum\limits_{e\in E}|w_e|\)次翻转后停止，但考虑到每条边长度输入的二进制编码，这实际上是一个指数级别的时间复杂度，当边权比较大时

最大割：Hopfield 中边权都是正的特殊情况

局部搜索可以得到一个超过最优解一半的局部最优解
存在一个 1.1382-近似算法
除非 P=NP，否则没有 1.0625(\(\dfrac{17}{16}\))-近似算法
Big Improvement Flip
- 近似比为\(2+\epsilon\)，会得到\((2+\epsilon)w(A,B)\geq w(A^*,B^*)\)的解
- 选取增长超过\(\dfrac{2\epsilon}{|V|}w(A,B)\)的 flip
- 最终会在\(O(\dfrac{n}{\epsilon}\log W)\)flip 后停下

13 Randomized Algorithms¶

略

14 Parallel Algorithms¶

EREW, CREW, CRCW
Merge, \(p=\dfrac{n}{\log n }\)

每隔\(\log n\)取一个计算 rank，这一步\(T=O(\log n),W=O(p\log n)=O(n)\)
根据这些取出来的划分出 2p 个子问题，规模为\(O(n/p)\),总时间复杂度\(O(\log n),\)总工作量\(2p\cdot O(\dfrac{n}{p})=O(n)\)
因此总\(T=O(\log n),W=O(n)\)

Maximum

Compare all the pairs \(T=O(1),W=O(n^2)\)

for Pi , 1 ≤ i ≤ n  pardo
    B(i) := 0
for i and j, 1 ≤ i, j ≤ n  pardo
    if ( (A(i) < A(j)) || ((A(i) = A(j)) && (i < j)) )
            B(i) = 1
    else B(j) = 1
for Pi , 1 ≤ i ≤ n  pardo
    if B(i) == 0
       A(i) is a maximum in A

workload 过大，因此首先考虑 partition

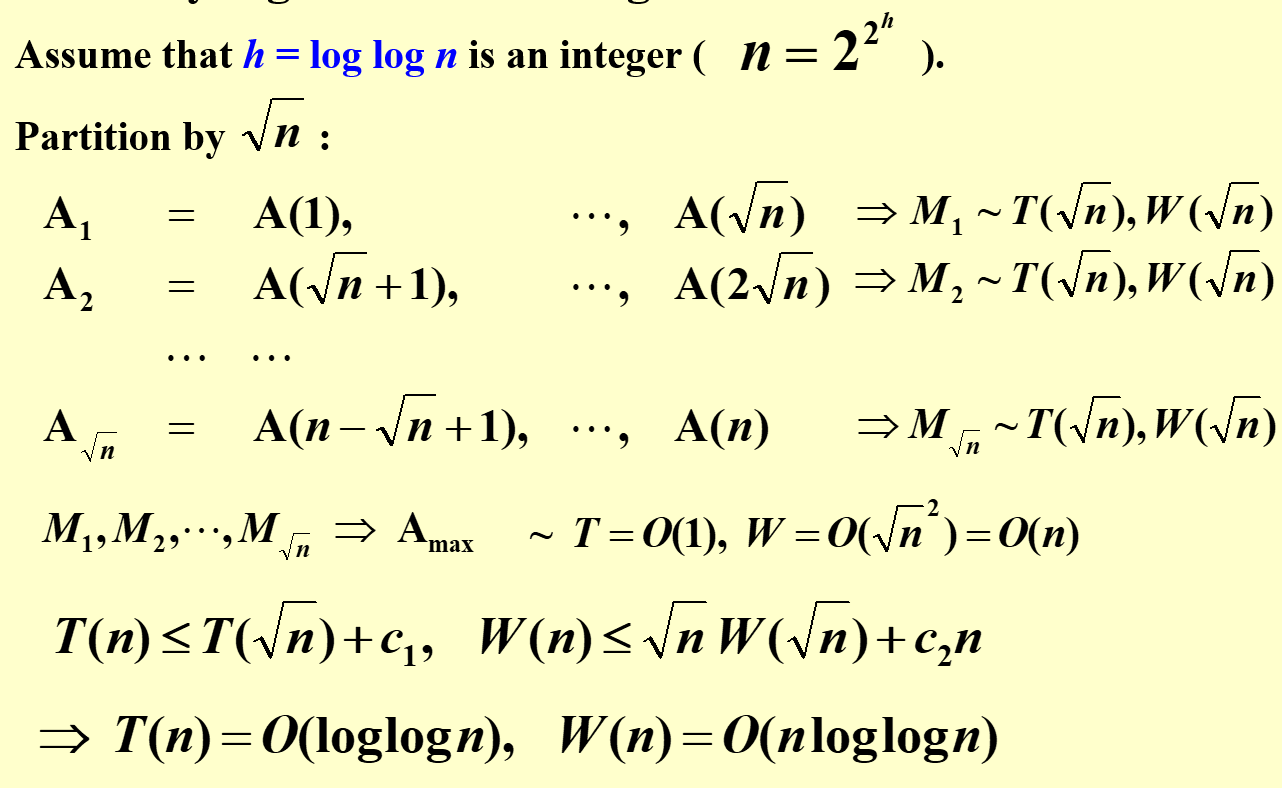
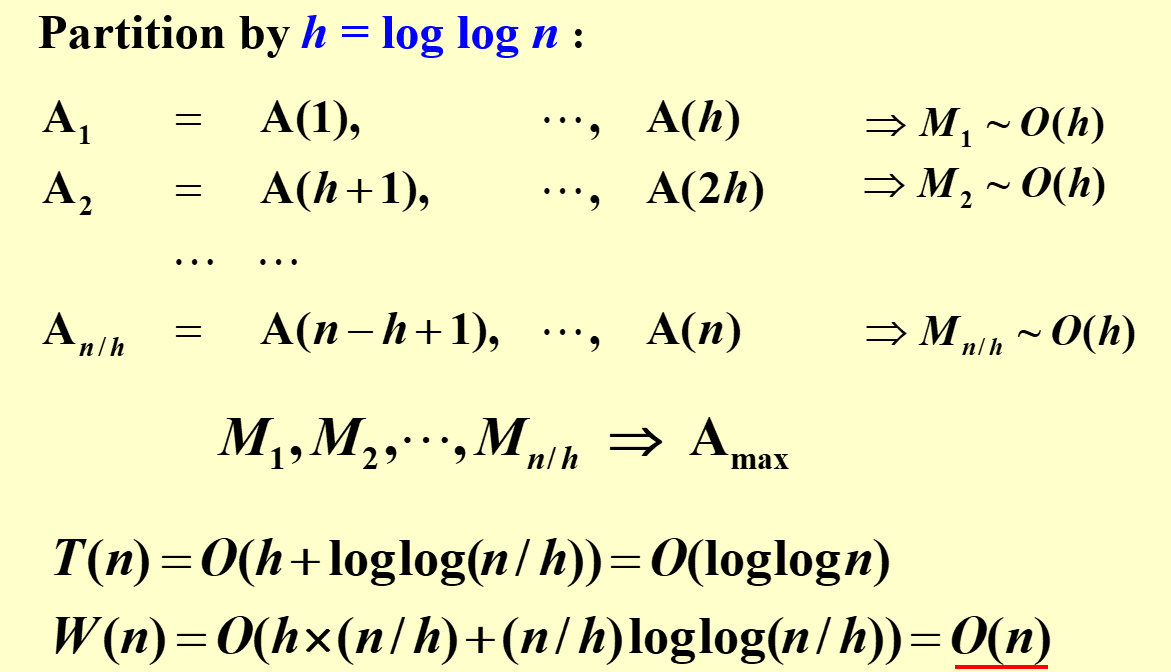
但有以下 Random Sampling，可以使得\(T=O(1),W=O(n)\)
- 取\(n^{7/8}\)个出来
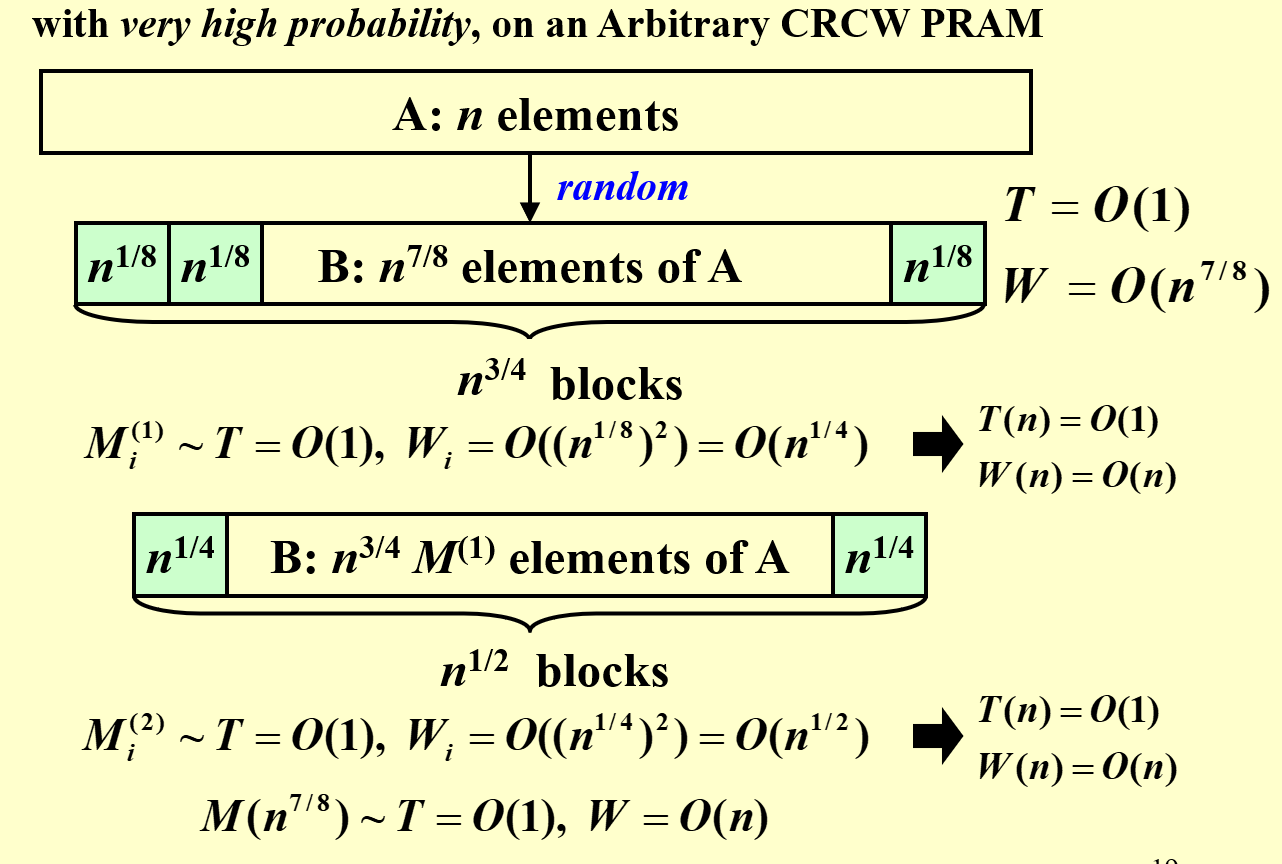
- 但这样最大值有可能不在其中，于是继续再取\(n^{7/8}\)个作为数组 B，下面步骤中若找到一个最大值，随机丢回 B 中的一个位置，因此是有可能把最大值覆盖掉的。但综合来看在上述时间内不能得到最大值的概率为\(O(\dfrac{1}{n^c})\),注意 c 是正常数

15 External Sorting¶

把每组排好序的记录叫做一个顺串(run)
一个 pass 表示一轮从输入磁盘到输入磁盘的工作，即所有元素都被移动（？
k 路合并需要\(1+\lceil\log_k\dfrac{N}{M}\rceil\)次的 pass，这个 1 是最初从 disk 读进来的
多相(Polyphase)合并:k 路合并只需要 k+1 的 tape，按 k 阶斐波那契数列 \(F^{(k)}(n)=F^{(k)}(n-1)+\cdots+F^{(k)}(n-k)\)分配

ADS Brief Review¶

1 AVL Tree, Splay Tree¶

2 Red-Black Tree and B+ Tree¶

Red-Black¶

B+¶

3 Inverted File Index¶

4 Leftist Heap and Skew Heap¶

Leftist Heap¶

Skew Heap¶

5 Binomial Queue¶

6 Backtracking¶

7 Divide and Conquer¶

8 Dynamic Programming¶

9 Greedy Algorithms¶

10 NP-Completeness¶

11 Approximation¶

12 Local Search¶

13 Randomized Algorithms¶

14 Parallel Algorithms¶

15 External Sorting¶

评论